记录 Heap 的算法实现

数据结构

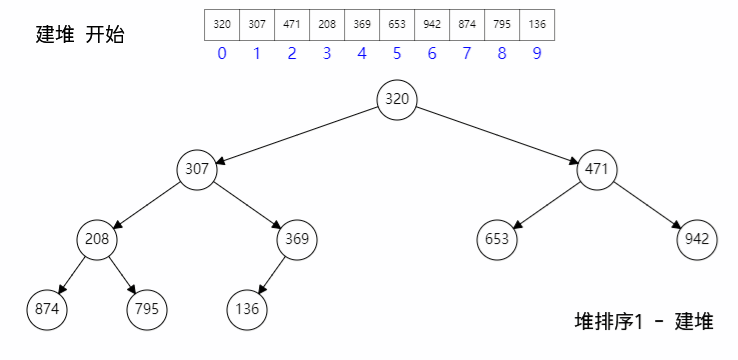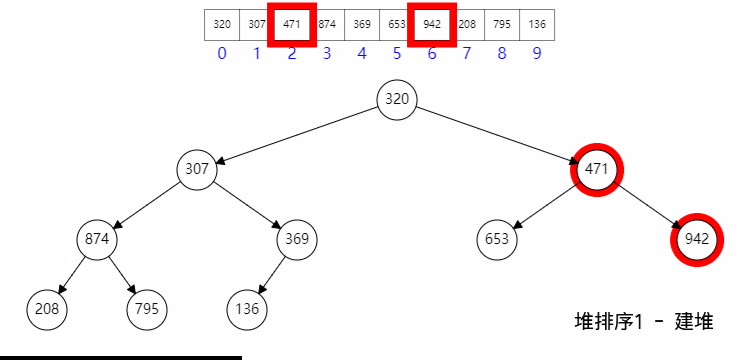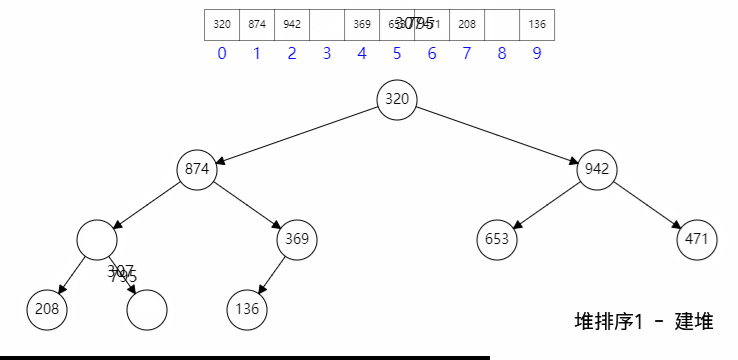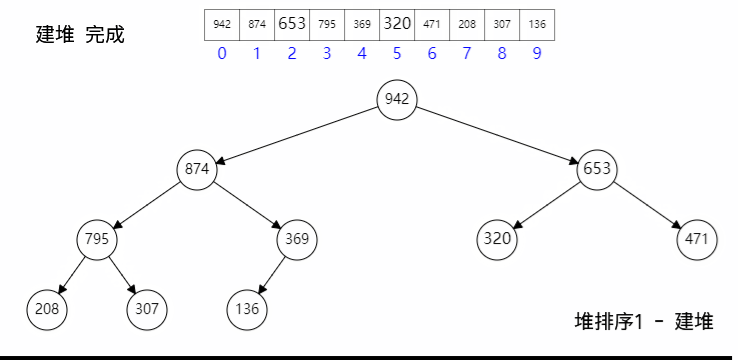一般我们说的 Heap 是指Binary Heap，即利用数组和二进制操作特性实现的二叉树结构，其中树顶(arr[0])可以是 Max 或 Min 值。

基本结构：
- 假设为 Min Heap，那么最小元素放在数组第一个元素 arr[0]
- 对于数组中下标为k的元素，它的两个孩子分别在2k+1和2k+2; 它的父结点在(k-1)/2
- Heapify(堆旋转)是 Heap 最核心的函数，只关心父结点和两个子结点间的关系要满足目标关系，比如目标是 Min，那么两个孩子必须都小于父，否则就要旋转交换，比如某孩子比父节点小，则孩子和父节点交换。如果发生了交换，那么发生变化的下标要继续向下递归 heapify
- 实际上 Heapify 的执行是有up和down两个函数实现的，up负责叶子元素发生变化后向上传递变化；down负责父结点变化后向下传递变化。
  - 注意边界条件，up的主体是子结点，所以cur>=1;down的主体是父结点，所以next<len
- heap 提供的 API：Init 初始化；Fix 中间某元素变化后修正；Push 增加元素；Pop 堆顶出堆；Peak 查看堆顶元素; Delete 删除某个元素
关于时间复杂度
- 对于一个完全二叉树，做 Heapify 操作时，乍看是O(nlogn)时间复杂度；但最底层数量占 1/2，逐层向上处理时规模按 2 的倍数快速收缩，所以整个过程时间复杂度是O(n)
- 如果构建 Heap 时是逐个元素构建的，那么时间复杂度是O(nlogn)，所以如果可以的话最好完整构建效率更高
- BuildO(n)
- Push/PopO(logn)
- DeleteO(n)
利用 Heap 可以实现Heap Sort
1. 对一个数组二分之一往上进行 Heapify，确保成为 Heap
2. 循环将头部元素和尾部交换，然后缩短 Heap 长度，直到所有元素处理完
3. Sort 的结果和 Heap 的类型刚好相反，例如 MinHeap，经过 sort 处理的数组为从大到小

题目

“502. IPO”

type hp struct {
    sort.IntSlice
}
func (p *hp) Less(a, b int) bool {
    return p.IntSlice[a] > p.IntSlice[b]
}
func (p *hp) Push(x interface{}) {
    p.IntSlice = append(p.IntSlice, x.(int))
}
func (p *hp) Pop() interface{} {
    ret := p.IntSlice[p.Len()-1]
    p.IntSlice = p.IntSlice[:p.Len()-1]
    return ret
}

func findMaximizedCapital(k int, w int, profits []int, capital []int) int {
    n := len(capital)
    sortedCap := make([][2]int, 0, n)
    for i := range capital {
        sortedCap = append(sortedCap, [2]int{capital[i], profits[i]})
    }
    sort.Slice(sortedCap, func(a, b int) bool {
        return sortedCap[a][0] < sortedCap[b][0]
    })

    h := new(hp)

    for capIndex := 0; k > 0; k-- {
        for ; capIndex < n && sortedCap[capIndex][0] <= w; capIndex++ {
            heap.Push(h, sortedCap[capIndex][1])
        }
        if h.Len() == 0 {
            break
        }
        w += heap.Pop(h).(int)
    }

    return w
}

“703. Kth Largest Element in a Stream”

type IntHeap []int

func (h IntHeap) Len() int {
    return len(h)
}

func (h IntHeap) Less(a, b int) bool {
    return h[a] < h[b]
}

func (h IntHeap) Swap(a, b int) {
    h[a], h[b] = h[b], h[a]
}

func (h *IntHeap) Push(x interface{}) {
    *h = append(*h, x.(int))
}

func (h *IntHeap) Pop() interface{} {
    res := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    return res
}

func (h IntHeap) Top() int {
    return h[0]
}

type KthLargest struct {
    size int
    intHeap *IntHeap
}
func Constructor(k int, nums []int) KthLargest {
    res := KthLargest{
        size : k,
        intHeap : (*IntHeap)(&nums),
    }
    heap.Init(res.intHeap)
    return res
}

func (this *KthLargest) Add(val int) int {
    heap.Push(this.intHeap, val)
    for this.intHeap.Len() > this.size {
        heap.Pop(this.intHeap)
    }
    return this.intHeap.Top()
}

// 手写 Heap
type KthLargest struct {
    nums []int
    k int
}

func (p *KthLargest) init() {
    for i := len(p.nums)>>1; i >= 0; i-- {
        p.down(i)
    }
}

func (p *KthLargest) down(cur int) {
    for next := cur<<1 + 1; next < len(p.nums); {
        if next+1 < len(p.nums) && p.nums[next] > p.nums[next+1] {
            next++
        }

        if p.nums[cur] > p.nums[next] {
            p.nums[cur], p.nums[next] = p.nums[next], p.nums[cur]
            cur, next = next, next<<1+1
        } else {
            break
        }
    }
}

func (p *KthLargest) up(cur int) {
    for next := (cur-1)>>1; cur >= 1 && p.nums[next] > p.nums[cur]; {
            p.nums[cur], p.nums[next] = p.nums[next], p.nums[cur]
            cur, next = next, (next-1)>>1
    }
}

func (p *KthLargest) push(x int) {
    i := len(p.nums)
    p.nums = append(p.nums, x)
    p.up(i)
}

func (p *KthLargest) pop() {
    n := len(p.nums)
    p.nums[0] = p.nums[n-1]
    p.nums = p.nums[:n-1]
    p.down(0)
    return
}

func Constructor(k int, nums []int) KthLargest {
    tmp := KthLargest{
        nums: nums,
        k: k,
    }
    tmp.init()
    return tmp
}

func (this *KthLargest) Add(val int) (ret int) {
    this.push(val)
    for len(this.nums) > this.k {
        this.pop()
    }
    return this.nums[0]
}

“295. Find Median from Data Stream”

type MyHeap struct {
    array []int
    isMax bool
}

func NewHeap(isMax bool) *MyHeap {
    return &MyHeap{
        array : []int{},
        isMax : isMax,
    }
}

func (h *MyHeap) Len() int {
    return len(h.array)
}

func (h *MyHeap) Less(a, b int) bool {
    if h.isMax {
        return h.array[a] > h.array[b]
    }
    return h.array[a] < h.array[b]
}

func (h *MyHeap) Swap(a, b int) {
    h.array[a], h.array[b] = h.array[b], h.array[a]
}

func (h *MyHeap) Push(x interface{}) {
    h.array = append(h.array, x.(int))
}

func (h *MyHeap) Pop() (x interface{}) {
    x = h.array[len(h.array)-1]
    h.array = h.array[0 : len(h.array)-1]
    return
}

func (h *MyHeap) Top() int {
    return h.array[0]
}

type MedianFinder struct {
    minHeap *MyHeap
    maxHeap *MyHeap
}

/** initialize your data structure here. */
func Constructor() MedianFinder {
    return MedianFinder{
        minHeap : NewHeap(false),
        maxHeap : NewHeap(true),
    }
}

func (this *MedianFinder) AddNum(num int)  {
    heap.Push(this.minHeap, num)
    // 注意这里要做一下流转，避免新元素造成大小顺序错误
    if this.maxHeap.Len() > 0 {
        heap.Push(this.minHeap, heap.Pop(this.maxHeap))
    }

    for this.minHeap.Len() > this.maxHeap.Len() {
        heap.Push(this.maxHeap, heap.Pop(this.minHeap))
    }
}

func (this *MedianFinder) FindMedian() float64 {
    if (this.minHeap.Len() + this.maxHeap.Len()) & 1 == 1 {
        return float64(this.maxHeap.Top())
    }
    return float64(this.minHeap.Top() + this.maxHeap.Top()) / 2.0
}