Algorithm Binary Indexed Tree

Posted on

记录 Binary Indexed Tree 的算法实现

数据结构

BIT(Binary Indexed Tree 树状数组)也叫 Fenwick Tree，可以快速求得数组前 n 项和，类似 preSum 数组的功能。

动作 preSum BIT
update(idx, delta) O(n) O(logn)
getSum(idx) O(1) O(logn)

如上所示，对于频繁变更数组元素的情况下 BIT 综合性能相比 preSum 高一个数量级。

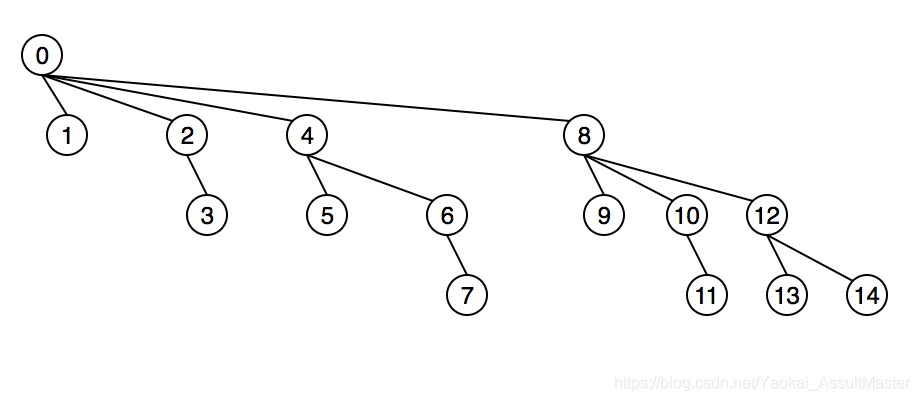BIT BIT 的实现方式类似 Heap，是在一个数组基础上实现类树状结构，不过这个树每个结点的出度不是固定的，会随着其二进制表示而变化。

  • BIT 的 childNode 的二进制表示，一定比 parentNode 多一个 1。
    • 0(b0) 没有 1，所以是树根
    • 1(b0001) 2(b0010) 4(b0100) 8(b1000) 都是在某位二进制有一个 1
    • 3(b0011) 5(b0101) 6(b0110) … 都是有两个二进制位为 1
  • BIT 的 childNode 的二进制表示，除了右边的最后一个 1 外，必定和 parentNode 相同
    • 4(b0100)作为 parent，5(b0101) 6(b0110) 作为 child 只比 4 多一位右边的 1

BIT

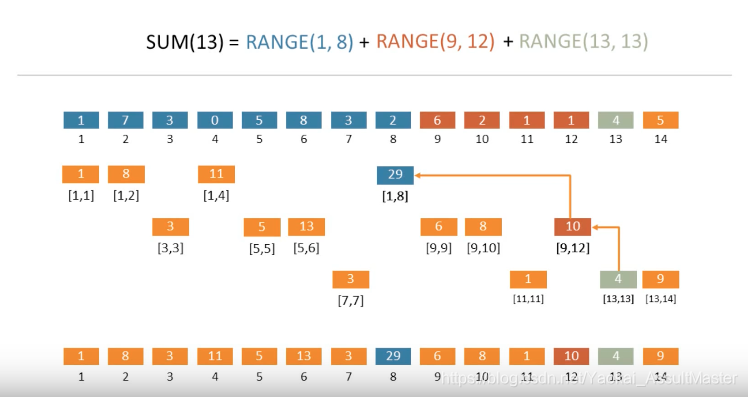
  • 上面关系只是描述了数组下标(index)的关系，真正的 RangeSum 是保存到每个元素的值，如上图，每个元素保存一段范围的和
  • 如图，最上面是原数组每个位置的值，最下面是 BIT 构建后结果数组的值
  • 同一个 parent 结点的 child 的值是 preSum 关系
    • 第一层 1 2 4 8 结点分别保存了原数组的 preSum 值
    • 第二层 4 的子结点 5 6 可以看出 preSum 关系
  • parent 的变化只影响同层的 preSum，不会影响 child
  • getSum(index)可以从目标结点向上遍历所有 parent 求和即可，如图getSum(13)的求和过程

  • update(index, delta)时需要把同层的变更结点的右边的 preSum 重算一遍，注意入参delta是原数的变动值，所以同时需要保存原数组

  • 实现细节：

    • 求当前下标最后一位可以用算法lowbit(x) = x & (-x)
    • 求 parent 下标可以去掉最后一位x - lowbit(x)
    • 求当前结点同层的右边下一个结点可以加上最后一位(最后一位位置会向左移，数值会更大)x + lowbit(x)，同时保证 x 不超过最大范围
    • 创建 BIT 时要指定容量，一般创建的数组容量比原数组最大值+1(类似 preSum 容量)，这样便于查询更新时直接用原数组下标操作，并且也能节省很多代码。 但是在查询和更新前注意初始下标值+1。

  • 任何能用 BIT 解决的一定能用 SegmentTree 解决，但是由于 BIT 实现简单，所以优先用 BIT

  • 小幅优化：
    • 在初始化时可以遍历添加元素，时间复杂度 O(nlogn)，也可以用下面算法优化为 O(n)
      1. 把所有元素拷贝至bit[1,n]的下标内
      2. 对所有元素循环处理，设当前下标为i令j = i + (i & -i)，bit[j] += bit[i]， 这个操作完成了两个动作：向同层元素右边累加 + 向上层元素累加
    • 有些情况下每次更新只需要元素计数+1，这种情况下无需 update 函数，只需要 increase 函数就可以了

示例： “307. Range Sum Query - Mutable”(模板) “315. Count of Smaller Numbers After Self” “327. Count of Range Sum” “493. Reverse Pairs”

题目

“307. Range Sum Query - Mutable”

class BIT {
    private:
    vector<int> bitree_;
    public:
    BIT (int maxNum) {
        bitree_.resize(maxNum + 1);
    }
    int getSum(int index) {
        int sum = 0;
        index++;
        while (index > 0) {	// 注意这里是 > 不是 >=，否则会造成死循环
            sum += bitree_[index];
            index -= index & (-index);
        }
        return sum;
    }
    void update(int index, int val) {
        index++;
        while (index < bitree_.size()) {
            bitree_[index] += val;
            index += index & (-index);
        }
    }
};
unique_ptr<BIT> pBIT_; // practice unique_ptr
vector<int> &nums_;
NumArray(vector<int>& nums) : nums_(nums) {
    pBIT_ = unique_ptr<BIT>(new BIT(nums.size()));
    for (int i = 0; i < nums.size(); ++i)
        pBIT_->update(i, nums[i]);
}
void update(int i, int val) {
    int diff = val - nums_[i];
    pBIT_->update(i, diff);
    nums_[i] = val;
}
int sumRange(int i, int j) {
    return pBIT_->getSum(j) - pBIT_->getSum(i - 1);
}

type NumArray struct {
    nums []int
    originNums []int
}

func (p *NumArray) init() {
    for i := 1; i < len(p.nums); i++ {
        if j := i + (i & -i); j < len(p.nums) {
            p.nums[j] += p.nums[i]
        }
    }
}

func (p *NumArray) update(index, delta int) {
    for index++ ; index < len(p.nums); index += index & -index {
        p.nums[index] += delta
    }
}

func (p *NumArray) preSum(index int) (ret int) {
    index++
    for index > 0 {
        ret += p.nums[index]
        index -= index & -index
    }
    return ret
}

func Constructor(nums []int) (ret NumArray) {
    ret.nums, ret.originNums = make([]int, 1, len(nums)+1), nums
    ret.nums = append(ret.nums, nums...)
    ret.init()
    return ret
}

func (this *NumArray) Update(index int, val int)  {
    diff := val - this.originNums[index]
    this.update(index, diff)
    this.originNums[index] = val
}

func (this *NumArray) SumRange(left int, right int) int {
    return this.preSum(right)-this.preSum(left-1)
}

“315. Count of Smaller Numbers After Self”

type BIT struct {
    nums []int
}
func NewBIT(n int) *BIT {
    return &BIT{nums: make([]int, n+1)}
}
func (p *BIT) Update(index, diff int) {
    for index++; index < len(p.nums); index += index & -index {
        p.nums[index] += diff
    }
}
func (p *BIT) PreSum(index int) (ret int) {
    for index++; index > 0; index -= index & -index {
        ret += p.nums[index]
    }
    return ret
}

func countSmaller(nums []int) []int {
    sorted := make([]int, 0, len(nums))
    sorted = append(sorted, nums...)
    sort.Ints(sorted)
    m := make(map[int]int)
    for _, num := range sorted {
        if _, ok := m[num]; !ok {
            m[num] = len(m)
        }
    }

    bit := NewBIT(len(m))
    ret := make([]int, len(nums))
    for i := len(nums)-1; i >= 0; i-- {
        ret[i] = bit.PreSum(m[nums[i]]-1)
        bit.Update(m[nums[i]], 1)
    }

    return ret
}

“327. Count of Range Sum”

type BIT struct {
    nums []int
}
func NewBIT(n int) *BIT {
    return &BIT{nums: make([]int, n+1)}
}
func (p *BIT) Increase(index int) {
    for index++; index < len(p.nums); index += index & -index {
        p.nums[index]++
    }
}
func (p *BIT) Sum(index int) (ret int) {
    for index++; index > 0; index -= index & -index {
        ret += p.nums[index]
    }
    return ret
}
func (p *BIT) Range(l, r int) (ret int) {
    return p.Sum(r) - p.Sum(l-1)
}

func countRangeSum(nums []int, lower int, upper int) (ret int) {
    n := len(nums)
    preSum := make([]int, n+1)
    allNums := make([]int, 1, 3*n + 1)
    for i, v := range nums {
        preSum[i+1] = preSum[i]+v
        allNums = append(allNums, preSum[i+1]-upper, preSum[i+1]-lower, preSum[i+1])
    }
    sort.Ints(allNums)
    m := make(map[int]int)
    for _, num := range allNums {
        if _, ok := m[num]; !ok {
            m[num] = len(m)
        }
    }

    bit := NewBIT(len(m))
    for _, sum := range preSum {
        ret += bit.Range(m[sum-upper], m[sum-lower])
        bit.Increase(m[sum])
    }
    return ret
}

“493. Reverse Pairs”

int res = 0, n = nums.size();
BIT bit(n + 1);
vector<int> v = nums;
sort(v.begin(), v.end());
unordered_map<int, int> m;
for (int i = 0; i < n; ++i)
    m[v[i]] = i + 1;
for (int i = n - 1; i >= 0; --i) {
    res += bit.getSum(lower_bound(v.begin(), v.end(), nums[i] / 2.0) - v.begin());
    bit.update(m[nums[i]]);
}
return res;

“1649. Create Sorted Array through Instructions”

type BIT []int

func (p *BIT) Update(index, delta int) {
    index++
    for index < len(*p) {
        (*p)[index] += delta
        index += index & -index
    }
}

func (p *BIT) PreSum(index int) (ret int) {
    index++
    for index > 0 {
        ret += (*p)[index]
        index -= index & -index
    }
    return ret
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

func createSortedArray(instructions []int) (cost int) {
    maxRange := 0
    for _, v := range instructions {
        if v > maxRange {
            maxRange = v
        }
    }
    const MOD = 1e9+7
    tmp := BIT(make([]int, maxRange+2)) // value as index may larger
    bit := &tmp

    for _, v := range instructions {
        cost += min(bit.PreSum(v-1), bit.PreSum(maxRange) - bit.PreSum(v))
        cost %= MOD
        bit.Update(v, 1)
    }
    return cost
}