记录 BFS 的算法实现

算法

`A*` (A star 启发式搜索)算法

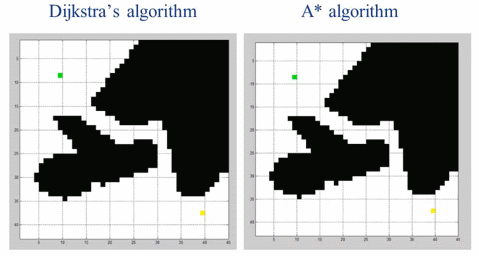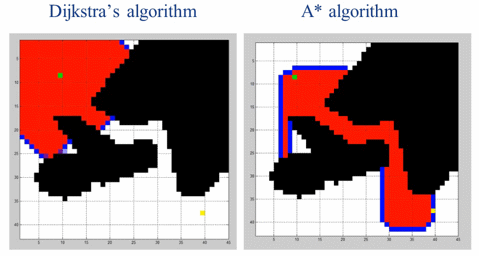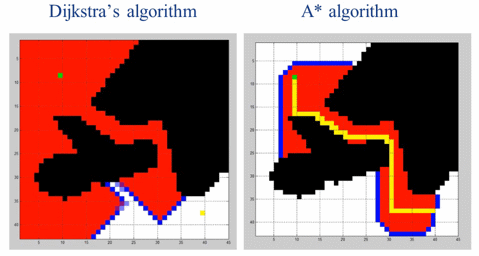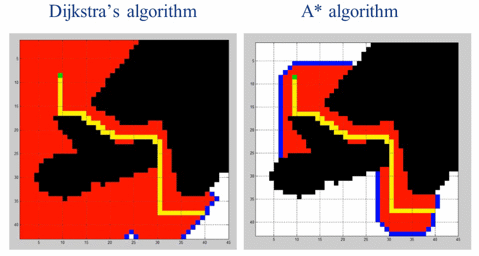
A*算法是在 BFS 基础上增加一个优化参数(Cost 代价值)，这样可以减少无效遍历，更快逼近目标。

算法思想：
- BFS 可以逐步在网格地图中找到目标，缺点是对各方向无差别遍历造成很大浪费； Dijkstra 可以在图中依照距离优先查找较近的目标，但如果是网格地图这种相邻结点无差别的情况下和 BFS 遍历路径是一样的，效率较低。 A*结合了网格 BFS 和 Dijkstra，适用于网格中已知起点和目标点的情况，对每个当前位置除了维护一个距离外还有一个”额外成本”，这个”额外成本”通常是”当前点到目标点”的距离，按照综合距离进行 Dijkstra 运算综合距离 = 当前距离+额外成本
A*算法也叫做启发式搜索算法，其中计算当前点到目标点的函数f(cur, target)称作启发函数
A*除了用于二维网格外，其实可以用于各种维度的 BFS
通常用某种距离(广义的空间中)作为启发函数
- 欧几里得距离(欧式距离) \(f((a1,b1),(a2,b2)) = \sqrt{((a1-a2)^2 + (b1-b2)^2)}\)
- 曼哈顿距离 \(f((a1,b1),(a2,b2)) = \left|a1-a2\right|+\left|b1-b2\right|\)
- 因为计算时无需开方效率较高，在A*中一般用曼哈顿距离
关于时间复杂度：
- 最大时间复杂度为O(nlogn)，其中 n 为网格数量
- 在网格路径搜索中，启发式搜索算法要明显好于 BFS 和 Dijkstra，上面的时间复杂度只能做参考
由于A*算法在实际应用中效率很高，所以常用于游戏地图中的寻路算法
A*并不适合所有场景，如果在搜索过程中存在空间虫洞(位置可以快速回退)，那么第一次找到目标的循环未必是最小步数。调整启发函数策略后，可能减少问题发生概率。如：”909. Snakes and Ladders”

示例： “752. Open the Lock”

题目

“752. Open the Lock”

// BFS
func openLock(deadends []string, target string) int {
    if target == "0000" {
        return 0
    }
    tarBytes := [4]byte{target[0],target[1],target[2],target[3]}
    deadSet := make(map[[4]byte]bool, len(deadends))
    for _, s := range deadends {
        if "0000" == s {
            return -1
        }
        deadSet[[4]byte{s[0],s[1],s[2],s[3]}] = true
    }
    memSet := map[[4]byte]bool{[4]byte{'0','0','0','0'}:true}
    queue := []ele{ele{value:[4]byte{'0','0','0','0'}, dist:0}}
    for len(queue) > 0 {
        cur := queue[0]
        queue = queue[1:]
        if cur.value == tarBytes {
            return cur.dist
        }
        for i := 0; i < 4; i++ {
            for j := -1; j < 2; j += 2 {
                tmp := cur.value
                tmp[i] += byte(j)
                if tmp[i] > '9' {
                    tmp[i] = '0'
                } else if tmp[i] < '0' {
                    tmp[i] = '9'
                }
                if deadSet[tmp] || memSet[tmp] {
                    continue
                }
                memSet[tmp] = true
                queue = append(queue, ele{value:tmp, dist: cur.dist+1})
            }
        }
    }

    return -1
}

type ele struct {
    value [4]byte
    dist  int
}

// A*
type astar struct {
    g, h   int
    status string
}
type hp []astar

func (h hp) Len() int            { return len(h) }
func (h hp) Less(i, j int) bool  { return h[i].g+h[i].h < h[j].g+h[j].h }
func (h hp) Swap(i, j int)       { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{}) { *h = append(*h, v.(astar)) }
func (h *hp) Pop() interface{}   { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

// 计算启发函数
func getH(status, target string) (ret int) {
    for i := 0; i < 4; i++ {
        dist := abs(int(status[i]) - int(target[i]))
        ret += min(dist, 10-dist)
    }
    return
}

func openLock(deadends []string, target string) int {
    const start = "0000"
    if target == start {
        return 0
    }

    dead := map[string]bool{}
    for _, s := range deadends {
        dead[s] = true
    }
    if dead[start] {
        return -1
    }

    get := func(status string) (ret []string) {
        s := []byte(status)
        for i, b := range s {
            s[i] = b - 1
            if s[i] < '0' {
                s[i] = '9'
            }
            ret = append(ret, string(s))
            s[i] = b + 1
            if s[i] > '9' {
                s[i] = '0'
            }
            ret = append(ret, string(s))
            s[i] = b
        }
        return
    }

    type pair struct {
        status string
        step   int
    }
    h := hp0
    seen := map[string]bool{start: true}
    for len(h) > 0 {
        node := heap.Pop(&h).(astar)
        for _, nxt := range get(node.status) {
            if !seen[nxt] && !dead[nxt] {
                if nxt == target {
                    return node.g + 1
                }
                seen[nxt] = true
                heap.Push(&h, astar{node.g + 1, getH(nxt, target), nxt})
            }
        }
    }
    return -1
}

“847. Shortest Path Visiting All Nodes”

func shortestPathLength(graph [][]int) int {
    // 当前下标(4bit) + 状态(12bit) + 当前距离(8bit)
    const STATE_MASK = 0b11111111111100000000
    const DISTANCE_MASK = 0b11111111
    n := len(graph)
    targetMask := ((1<<n) - 1)<<8

    m := make(map[int]bool, n)
    q := make([]int, n)
    for i := 0; i < n; i++ {
        next := (i<<20)|(1<<(i+8))
        q[i] = next
        m[next] = true
    }

    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        idx, curMask, dist := cur>>20, cur&STATE_MASK, cur&DISTANCE_MASK
        if curMask == targetMask {
            return dist
        }
        for _, next := range graph[idx] {
            nextMask := (next<<20)|((1<<(next+8))|curMask)
            if !m[nextMask] {
                q = append(q, nextMask|(dist+1))
                m[nextMask] = true
            }
        }
    }
    return 0
}

“1036. Escape a Large Maze” Golang

func isEscapePossible(blocked [][]int, source []int, target []int) bool {
    blockMap := make(map[Point]struct{})
    for _, b := range blocked {
        blockMap[Point{b[0], b[1]}] = struct{}{}
    }
    return bfs(Point{source[0], source[1]}, Point{target[0], target[1]}, blockMap) && bfs(Point{target[0], target[1]}, Point{source[0], source[1]}, blockMap)
}

type Point [2]int
func bfs(source Point, target Point, block map[Point]struct{}) (ret bool) {
    dir := [][]int{ {-1, 0}, {1, 0}, {0, -1}, {0, 1} }
    visited := map[Point]struct{}{source:struct{}{}}
    l := list.New()
    l.PushBack(source)
    steps := 0

    for l.Len() > 0 && steps < 20000 {
        cur := l.Remove(l.Front()).(Point)
        steps++
        if cur == target {
            return true
        }

        for i := 0; i < 4; i++ {
            next := Point{cur[0]+dir[i][0], cur[1]+dir[i][1]}
            if next[0] < 0 || next[1] < 0 || next[0] >= 1e6 || next[1] >= 1e6 {
                continue
            } else if _, exists := block[next]; exists {
                continue
            } else if _, exists := visited[next]; exists {
                continue
            }
            visited[next] = struct{}{}
            l.PushBack(next)
        }
    }
    if steps >= 20000 {
        return true
    }
    return false
}

算法

A* (A star 启发式搜索)算法

题目

“752. Open the Lock”

“847. Shortest Path Visiting All Nodes”

“1036. Escape a Large Maze” Golang

`A*` (A star 启发式搜索)算法