记录常用算法技巧

基本概念

O(Big O) 表示随问题元素数量增加，所需步骤/空间的增加速度。
- 常见的有：
  - exponential(指数的) 比如 dfs
  - polynomial(多项式的) 如 O(n)、O(n^2)
  - linear(线性的) 等价于 O(n)
  - 对数的(logn) 比如二分查找
    - 这里的$logn$实际上是$log_2n$(以 2 为底 n 的对数)
TLE Time Limit Exceeded，算法执行时间超过限制
Pseudo Code 伪代码，只表达核心逻辑，并不能编译运行的代码

做题流程

看清题意，理解问题，看懂给定的 case。提前准备纸笔，可以用来画图和模拟演化。
记录给定的 case、自己创建可能发生的情况的 case（如：数组为空、参数越界、前后顺序差异、重复变量…），存储在临时文本位置。如果有 case 不确定正常返回值，可以填写默认返回值，测试一下想到的 case，如果期待结果是报错的，说明不会有这个 case。
做题，将上面所有的 case 跑通。如果思路没问题，可以先将主要逻辑写出来，然后再考虑边界情况。如果发生错误，修改后，跑通当前 case 以及可能影响的 case。
确保没有问题后，修正格式、有意义的变量名、函数名、加上关键注释、删除 log 输出、删除无用注释，重新跑一遍所有 case。
最后提交代码。真正的线上笔试只能提交一次，提交一次就成功与提交很多次的难度不在一个数量级，所以要以一次提交成功为目标进行练习。

其他技巧

一道题认真思考 10 分钟还解不出就直接看答案思路，没必要一直钻牛角尖
关于规模和解法，通常解法时间复杂度和对应的元素规模上限如下：
- O(n^n), 40
- O(n^3), 500
- O(n^2), 1000
- O(n), 1e7
- O(logn), infinit
  - 可以看出 logn 的性能基本接近常数，是算法尽量追求的目标
- O(mlogn), 1e5, 1e9
leetcode 运行时报错，一般都是数组越界。有时也是空指针问题。
在逻辑较为复杂时，可以先将逻辑嵌套写出来，然后再进行精简。一上来就精简可能会造成逻辑复杂，导致 case miss。
在 double 型运算中，通常用 eps = 1e-6(10^-6)为期望(expects)测精度。
leetcode 中经常要对 1000000007 取模，可以简写为 const int MOD = 1e9+7，之所以取这个数是因为它是最大的一个质数。
要谨慎使用全局变量，如果函数会被调用多次，未重置的全局变量会导致提交失败
需要用到rand()函数时，leetcode 会对该函数做延迟处理，调用过多时即使时间复杂度接近(比如 O(4n)->O(n))，算法也会超时
图形类的，可以用手画一画演化过程，寻找规律。例：”48. Rotate Image”
关于迷宫题，看清楚题目，是全部踩一遍还是最短路径。
一般 Contest 时需要直接 copy 数据结构模板，或者快速背写出来
注意题目中的名词：
- SubString(子串)是连续的元素
- SubSequence(子序列)是非连续元素

C++ 技巧

除非是题目留下的题目类本身的构造函数，不要自己去重新写构造函数，可能会有问题。
有时”Run Code”和”Submit”检测结果不同，这时，很可能是某些变量没有初始化，在”Run Code”时由于是 Debug 模式，所以自动赋了初值，而”Submit”时没有初始化导致的。
在 leetcode 中，可以通过 cout 输出 log。
在 leetcode 中，认为红黑树的创建、遍历过程为O(nlogn*) ≈ O(n)，红黑树被广泛应用于 set、map 系列中。

Golang 技巧

可以用fmt.Println(x)来输出 log
可以用fmt.Printf("%b", x)输出二进制
leetcode 运行 Go 代码时，报”Runtime error”，一般是有死循环了。

数据结构

Array(数组)

多维数组

一般可以用二维数组表示地图或者用多维数组表示更复杂的映射关系。

算法：BinarySearch(二分查找)

Binary Search 模板

利用数组的有序(默认升序)特性，在O(logn)时间复杂度内找到答案。

二分查找的要点:
- 每次通过nums[mid]和target的关系丢弃另一半不需要考虑的区域，缩小边界范围
- 每次修改范围时边界条件和变更值一致，具体的说是考虑=的情况。
- 最后考虑返回的结果和 l、r 的关系

例：“33. Search in Rotated Sorted Array”

由于二分查找性能极好，经常在其他算法中可以用于猜数字。只要某个数字具有这种特性：超出一某个值后，某个判断就会一直成立，小于这个值就一直不成立；或者反过来，超出某个值后条件就不成立。比如猜 SlidingWindow 的 Window 长度等

示例： “1044. Longest Duplicate Substring” SlidingWindow RollingHash “1723. Find Minimum Time to Finish All Jobs” BinarySearch

LowerBound

lower_bound(begin, end, num) 从数组的 begin 位置到 end-1 位置二分查找第一个大于或等于 num 的数字，找到返回该数字的地址，不存在则返回 end。

在 C++中，可以用lower_bound实现

lower_bound(a + 1, a + 1 + n, x, cmp);
bool cmp(const int& a,const int& b){return a > b;}

在 Go 中，可以用sort.Search实现

示例： “74. Search a 2D Matrix” Array Golang

UpperBound

upper_bound(begin, end, num) 相比 LowerBound 算法使用较少，从数组的 begin 位置到 end-1 位置二分查找第一个大于 num 的数字，找到返回该数字的地址，不存在则返回 end。

环状 array 技巧

通常 array 的特点是可以随机向后 n 步跳转，增加环状条件后，跳转的目标位置可以通过取余计算得到
如果 array 的边界处理非常复杂，可以将数组复制成多个有限长度的数组，其长度也可以是原数组的两倍，然后分别在不考虑边界条件的情况下求解，最后综合各个数组综合取得结果示例：”213. House Robber II”

前缀和压缩(prefix sum)

可以利用前缀和 dp 结果做一维压缩，通过任意两点可以计算中间的和。示例：

进一步，可以在二维数组中对一维再压缩一次，通过两个点快速计算矩形内元素和。示例： “363. Max Sum of Rectangle No Larger Than K” Array “497. Random Point in Non-overlapping Rectangles” Random “528. Random Pick with Weight” Random

preSum 还可以用于二进制异或运算 示例：“1310. XOR Queries of a Subarray” BinaryOperation
计算二维 preSum 有两种算法：
1. 普通的 preSum 累加：先从左到右再从上到下累加
2. DP: 根据二维 preSum 的相邻关系有转移方程：dp[i][j] = matrix[i-1][j-1]+dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]，注意这里 matrix 的长度比 preSum 小 1，所以下标要-1，即左边、上边都累加了左上的元素和，所以要减掉

示例：“1738. Find Kth Largest XOR Coordinate Value” BinaryOperation

preSum 还可以用于RollingHash

示例：“1316. Distinct Echo Substrings” SlidingWindow RollingHash

差分(diff array)

差分是 prefix sum 的反向逻辑处理，类似 line sweep，在 diff 数组修改起始结束点的值以达到修改 prefix sum 结果的目的。

示例： “1109. Corporate Flight Bookings” Array

Kadane 算法(最大连续字段和)

Kadane 是经典的最大连续字段和算法，代码如下：

ans = cur = None
for x in A:
    cur = x + max(cur, 0)
    ans = max(ans, cur)
return ans

示例： “918. Maximum Sum Circular Subarray” Array

Heap(堆)

一般说的堆都是Binary Heap，利用数组和二进制关系实现的二叉树结构。堆可以是最大堆或最小堆，由 compare 规则决定。由于具有二叉树的特性，Heap 可以在 O(logn)时间复杂度内完成一次最大值/最小值查找，实现也不困难。

堆常用于Priority Queue的实现，是性能最好的 PQ

具体实现参考： Heap

示例：“703. Kth Largest Element in a Stream” Heap Golang

LinkedList(链表)

单向链表、双向链表、环状链表(Ring)

链表和 Tree 非常相似，都是以指针相关联，可以利用 DFS 或逐个元素遍历进行处理

算法：归并排序

归并排序可以用于顺序数据结构(数组、链表)，用一个额外的空间对已有序子数组进行合并。时间复杂度 O(nlogn)，空间复杂度 O(n) 在某些数据量巨大、无法加载到内存的情况下是唯一可用算法。

示例： “88. Merge Sorted Array”

算法：快慢指针法(Tortoise and Hare)

用于判断链表中是否存在回路，以及交叉点的位置。

对于一个有向单链表或类似的可形成环装的结构，为了判断是否存在回路(loop)，可以分别用快、慢指针遍历，快指针每次走两步、慢指针每次走一步，如果快指针与慢指针在某个位置重叠了，说明存在回路。

例:”457. Circular Array Loop”、”141. Linked List Cycle”。

对于需要快速跳转到单链表结尾判断长度，并从中间开始操作的情况，也可以使用快慢指针法。

例：”234. Palindrome Linked List”。

技巧：添加辅助头节点

遍历处理链表时往往头节点的处理非常复杂，可以 new 一个辅助 dummyHead 节点，设置合适的 Val 值，将 Next 设置为原 head，这样就可以无差别遍历了。

示例： 82. Remove Duplicates from Sorted List II Golang

链表相交点

可以人为修改两个链表的遍历过程，从中发现相交特定，具体算法参考： “160. Intersection of Two Linked Lists”

利用相邻结点保存关联关系

可以利用链表紧邻的结点存储额外关联关系

“138. Copy List with Random Pointer”

DFS 处理每个结点

可以利用 DFS 处理每个结点，通过控制 cur 和 next 在 DFS 的执行顺序，实现正序/逆序处理。

示例： “138. Copy List with Random Pointer” “206. Reverse Linked List”

Stack(栈)

符合 FILO(先进后出)，从栈顶入从栈顶出

算法：Monotone Stack(单调栈)

可以在遍历过程中保存到目前为止的一系列有序极值

示例： 456. 132 Pattern 1063. Number of Valid Subarrays

stack 背影法

有些时候利用 stack 追溯过去元素时，要看到之前的有效范围，这时在无用元素 pop 后，可以看到的 top 就是前面的”背影”。

例：”84. Largest Rectangle in Histogram”、”32. Longest Valid Parentheses”

多个栈配合

有时需要多个栈配合实现算法

示例：
- 两个各自存储信息，动态决定选取哪个栈顶元素 “678. Valid Parenthesis String” Stack

Queue(队列)

符合 FIFO(先进先出)，一般从队尾入队，队首出队

DQueue(double queue，双向队列、双端队列)

dq 可以同时提供两个 queue，一个 queue 的队首是另一个的队尾。 dq 兼有 stack 和 queue 的功能，在 front 端可以进行时间或范围的检查并弹出，在 back 端可以对可忽略值进行弹出。

C++ STL 的 deque 实现比较好，底层用多段数组实现
也可以用 linkList 代替，只要使用 linkList 操作接口子集就可以
用 C++的 vector 或 Go 的 slice 也可以实现，但是队首出队后空间会被浪费

示例：例：”239. Sliding Window Maximum”、”918. Maximum Sum Circular Subarray”

算法：Monotone Queue(单调队列)

单调队列用 dq 实现，队列中的元素始终保持有序，队首始终保持最值。队首元素按顺序出队、队尾元素可以在遍历过程中入队或出队来维护队列元素值有序。

示例： “1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit” SlidingWindow+MonotoneQueue Golang

Priority Queue(PQ)

PQ 是一种具有优先级排序的队列，在相同优先级下和 Queue 相同 FIFO；但是如果有不同优先级的元素，则优先级更高的元素先出队。

PQ 可以有多种实现方案，一般都是能够新增元素时自动有序的容器，如 Heap、平衡二叉树等

Heap(堆)

Heap 是一种自动排序的容器，利用数组和有序二叉树的关系实现。

Heap 延迟删除

由于 Heap 的特性是只能删除堆顶元素，但是有时做统计时需要删除堆内元素，这种情况可以利用一个 HashMap 记录已删除的元素和数量，另外需要独立记录真实 size。

示例： “480. Sliding Window Median” StructDesign

Tree(树)

Tree 的结构特点决定了非常适合用 DFS 算法进行遍历，注意未必只遍历一次，可以以不同的方式遍历多次获得答案。

Tree 可执行的操作：
- 通过 DFS，前/中/后序遍历
- 寻找目标结点
- 寻找公共父节点=
- 通过 DFS 调用传递层级等参数

Binary Tree（二叉树）

以二叉树为基础衍生出：完全二叉树(每一级孩子最多为 2k 个)、搜索二叉树(Binary Search Tree 查找树)、自平衡二叉查找树（AVL Tree）、红黑树（BlackRedTree）等，所以对二叉树的结构要非常熟悉。二叉树的基本操作是插入、遍历，其中遍历有 pre-order(先根遍历)、in-order(中根遍历)和 post-order(后根遍历)。只要有两种遍历顺序，就可以确定一个二叉树的结构。搜索二叉树中序遍历正好是有序数组，所以搜索二叉树可以用来排序，时间复杂度为 O(logn)。

完全二叉树的特征：设有 n 层，第 k 层(下标从 0 计算)的元素数量为2^k，叶子结点数量 = 非叶子结点总数 + 1
树可以用数组实现，利用父子结点下标间的关系
也可以用结点指针实现

BST(Binary Search Tree 二叉搜索树)

特性：
- 左子树所有值小于当前结点、右子树所有值大于当前结点
- 中序遍历输出(左中右)正好是顺序
优点：
- 可以对元素进行二分查找
缺点：
- 没有自动平衡能力，可能元素不多但深度很深，查找效率降致 O(n)

Balanced BinaryTree(平衡二叉树)

BST 的缺点是没有平衡能力，即相同的存储元素集合，由于插入顺序不同会形成不同的树结构，比如一直从小到大插入，会形成一个”偏树”，层级很高而元素数量很少。这种情况下 CRUD 性能会从 O(logn)下降为 O(n)。

为了应对这种问题，提出了平衡二叉树也叫 AVL-Tree。可以在每次插入和删除时进行平衡旋转操作，从而降低高度，提高效率。

AVL-Tree 相对较复杂，所以这里就不列出旋转逻辑了。

Treap(Tree Heap 树堆)

Treap 是一个二叉搜索树，同时保持堆的结构，在插入时通过随机值实现了自动随机平衡功能。

Treap 查询过程和普通的 BST 是一样的，差别是在插入、删除后进行堆维护旋转
插入过程：
1. 插入新元素时，除了元素本身的值，结点上要加一个随机优先级 priority
2. 插入先按照一般的 BST 插入，然后根据 priority 进行堆维护旋转
3. 假设维护一个最小堆，如果当前结点是父结点的左子结点同时 priority 小于父结点，那么就进行右旋；反之左旋
4. 一路旋转直到满足最小堆的条件不再旋转，由于旋转不破坏 BST 的顺序性，所以最终结果仍然是 BST
由于每次插入 priority 都是随机的，可以很好的打破 value 本身的顺序导致深度过高问题，利用概率实现了平衡
Treap 的 CRUD 期望时间复杂度均为 O(logn)，性能非常好
通过随机实现自动平衡，所以相比 AVL-Tree，旋转要更容易(只需左/右旋转)，代码更容易实现，适合 Golang

实例： “213. House Robber II” OrderedMap Treap Golang

TrieTree(Prefix Tree 前缀树)

特里树/前缀树，读作”try tree”，用于在已知字典中快速查找目标字符串是否存在或者是否匹配前缀，广泛用于动态搜索框、高性能字符串查找。

数据结构关键：
- 树中结点的成员：isEnd标志是否找到目标字符串、childs以 HashMap 的方式映射到下一层结点，map 的 key 就是本层可以匹配到的元素
- 整个树从跟结点开始
- 树需要先构造再使用
- 提供”查找元素”、”匹配前缀”两种功能
优化：
- 如果每个位置的元素范围较小，比如”所有数字/小写字母”，那么可以利用数组代替 HashMap，提高效率

实例： “208. Implement Trie (Prefix Tree)” TrieTree Golang “212. Word Search II” TrieTree Golang

BinaryIndexTree(索引树)

BIT (树状数组 Binary Indexed Tree/Fenwick Tree)。提供getSum(i)和update(i,val)函数，可以获取目标数组第 i 位置(包括)往前所有元素的和(可以求和也可以求范围内最大或对小值)，可以动态更新某位置的值。

getSum和update的时间复杂度都是 O(logn)。如果用一般的遍历方法求 sum，时间复杂度是 O(n)，更新一个值的时间复杂度是 O(1)；如果我们用 dp sum 的方式来实现 sum 的快速查询，那么查询的时间复杂度是 O(1)，但更新一个值的时间复杂度是 O(n)相比较 O(logn)较差。

使用 BIT 适用于查询和更新频繁度相当的情况，可以降低总的时间复杂度。具体实现方法参照： “307. Range Sum Query - Mutable” Binary Indexed Tree C++。

注意点：
1. 有一种叫 Segment Tree 的类似结构，功能与 BIT 相同但是代码更复杂，不易使用。
2. 在实现 BIT 时，一般创建的数组容量比原数组最大值+1，这样便于查询更新时直接用原数组下标操作，并且也能节省很多代码。但是在查询和更新前注意下标值+1。
3. BIT 要求输入的位置范围为 0~n。有时，输入数组并不是紧凑在一定范围，非常稀疏，或者可能出现负数。这种情况下，可以利用一个 convert 转换，将原数组排序后，每个元素存入 BIT 的下标为排序后的顺序号(下标+1)，这样就可以连续而保持正整数了。如：{7, -90, 100, 1} => {3, 1, 4 ,2 }。转换函数参考：“315. Count of Smaller Numbers After Self” Binary Indexed Tree C++。

BIT 应用案例： “493. Reverse Pairs” Binary Indexed Tree C++、“315. Count of Smaller Numbers After Self” Binary Indexed Tree C++

ST(SegmentTree 线段树)

Segment Tree 的功能与 BIT 类似，代码更为复杂，但是逻辑较为直观。 Segment Tree 是一个二叉平衡树，所以更新和查找性能较好。每个叶子节点(segment)代表真正的值，非叶子节点是其子节点范围内合并的值。

Segment Tree 和 BIT 都是在开始时确定规模，然后基本结构不再改变，只是逐个更新和求和计算。

各函数时间复杂度：
- build(start, end, vals) -> O(n);
- update(index, value) -> O(logn);
- rangeQuery(start, end) -> O(logn + k); k 是与规模有关的一个值，通常不会太大。
ST 有三种实现形式：
- ST array 实现版
- ST treeNode 实现版(推荐)，思路简单，但是代码较多
- ST zkw 版，实现简单、逻辑精巧，但是难以解释

具体代码参照： “307. Range Sum Query - Mutable” SegmentTree C++

相比 BIT ST 除了 rangeSum 功能外，还可以实现 rangeMin/rangeMax

Red Black Tree (红黑树)

红黑树广泛应用于 map、set、multimap、multiset、priority_queue 系列中，红黑树是一种平衡二叉树元素是有序的，与一般的 AVL 树（自平衡二叉查找树）的优势在于具有极高的统计性能，可以始终保持 insert、get、erase 的时间复杂度都为O(logn*)，在 n 的数量足够大时，可以认为时间复杂度为 O(1)（log 曲线趋平），所以有些需要达到 O(1)、O(n)等极限性能的情况可以利用这种数据结构。

如：”432. All O`one Data Structure”

HashTable

Hashtable（哈希表），被广泛应用于 unordered_map、unordered_set、unordered_multimap、unordered_multiset 中， insert、get、erase 的时间复杂度都为 O(1)，适合要求极限性能的情况，但是元素是无序的。

缺点是空间使用较多，要预留很多 bucket。

Longest Consecutive Sequence (最长连续子串)

求数组或字符串(字符数组)的某段连续字串，具有某种性质，规模往往超出1e3无法用O(n^2)解决。

算法：preSum + HashMap
- 步骤：
  1. 遍历计算 preSum，preSum 经过计算得出某种特征值，将特征值保存在 HashMap 中，同时记录下标
  2. 如果特征值已存在，则说明到上次出现此特征值中间的子数组符合题目要求，计算两者下标差统计一次结果
  3. 在特征值已存在的情况下就不要再更新特征值，这样可以统计到最长结果

示例： “1. Two Sum” “128. Longest Consecutive Sequence” “523. Continuous Subarray Sum” “525. Contiguous Array”

结合 Array 实现 O(1)容器

“380. Insert Delete GetRandom O(1)” StructDesign “381. Insert Delete GetRandom O(1) - Duplicates allowed” StructDesign

Ordered Map(有序 Map)

有序 Map 的实现方式可以有多种，效率较高的有：AVL-Tree、Treap(Golang)、Skiplist(Redis)、RedBlackTree(C++ STL)

OrderedMap CRUD 各项操作的时间复杂度是 O(logn)，适用于在遍历过程中要不断保持顺序的情况。

如：“253. Meeting Rooms II”

Graph(图)

图是指多个节点相关联的数据结构，可以分为有向图和无向图。我们说的图默认是指有向图，无向图可以看作是边是双向的有向图。树是一种特殊的图，它相当于图中元素全部可以直接或间接联系在一起，但是不存在环状结构。图的存储可以有多种形式，比如用边数组存储、hashtable 存储边、用矩阵存储，可以根据实际情况转换存储方式。如果是树的话，还可以用树形结构的节点对象存储。

DAG(Direct Acyclic Graph)有向无环图

如：“277. Find the Celebrity”Graph C++

最短路径

算法名	场景	时间复杂度
Dijkstra’s	从一个结点到所有结点的最短路径，路径必须是正数	O(V^2)
Bellman-Ford	从一个结点到所有结点的最短路径, 路径可以为负数	O(VE) or O(V^3)
Floyd-Warshall	各结点之间的最短路径，路径可以为负数	O(V^3)

Relax 在遍历更新每个结点对应的距离时，会逐步逼近结果，这个过程叫 Relax(松弛)操作

示例： “743. Network Delay Time” Graph “787. Cheapest Flights Within K Stops” Graph

Dijkstra(狄杰斯特拉)

dijkstra 求得图中起始点到各个可达点的最短距离，并且它检索到某点第一次时就是到那点的最短距离。利用优先级队列存储当前探索的点的序号和当前检索到这点的距离，按照距离最短进行优先级排序。

步骤：
1. 最初优先级队列中推入起始点，然后将当前点的下一可达位置及距离推入队列，距离越短优先出队。
2. 中途通过一个数组存储起始点到所有点的距离，默认为 INT_MAX。
3. 最后该数组就是目标数组，如果还有 INT_MAX 值，说明这点不可达。

Bellman-Ford

求指定起点到其他地点的最短距离，输入的边不可以形成negtive cycle

步骤：类 DP
1. 创建起始点到图中所有定点的集合(比如一个数组)，起始点到自己的距离是 0，其他默认距离是 MaxInt
2. 计算最短路径循环，执行V-1次遍历(类似 bubbleSort)。循环中遍历所有的边，如果起点 u 的距离 du 加上边的权值 w 小于终点 v 的权值 dv，则更新 dv = du。为了避免后效性，每轮循环都要从之前的 dp 数组clone出一个临时数组进行更新操作。(无法通过对 edges 排序消除后效性)
3. 最后检测图中是否有负权边形成了环。遍历途中所有边，计算 u 至 v 的距离，如果对于 v 存在更小的距离，说明存在负环。

Floyd-Warshall

求任意两点之间的最短路径

步骤：
1. 首先将图保存为可以快速查询两点之间距离的存储形式，例如 Ajacent Metrix(邻接关系矩阵)。结点和自己的距离是 0；如果有已知距离则赋值；未知距离填写正数最大值；
2. 三层循环 k、i、j，k 表示尝试插入的结点，i 表示起点，j 表示终点，循环尝试将 k 插入 i->j 中间时是否有更近的距离，如果有则记录

Topological Order(拓扑排序)

如果数据关系可以形成一个有向无环图，那么可以用拓扑排序形成一个唯一顺序序列，BFS 是比较常用的方法。

排序方法：
1. 选择一个入度为 0 的顶点，输出它，并在图中删除。
2. 删除这个定点对应的边。
3. 不断循环 1、2，直到结束。
4. 如果输出的顶点数小于总顶点数，则说明有回路; 否则，输出的序列就是拓扑排序结果。

例： “207. Course Schedule” “269. Alien Dictionary” “310. Minimum Height Trees” Graph C++

DSU（Disjoint Set Union 并查集）

并查集也叫 UninFind，提供 find(查找)和 union(合并)函数，适合于将大量元素(例如无向图的节点)分为不同的集合、动态合并集合，最终根据集合关系、集合容量得到答案。

DSU 的性能非常高，增加了 rank 优化后时间复杂度可以达到 O(1)。
DSU 使用的注意点：
1. 要把所有初始数据遍历输入到 DSU 中，再判断结果，中间结果是不完整的(有些关联还没有建立)。
2. 注意 DSU 中有很多孤立节点，输出结果要考虑到这些孤立节点是否计数。

例：”924. Minimize Malware Spread”、”684. Redundant Connection”、”947. Most Stones Removed with Same Row or Column”、”721. Accounts Merge”

Euler tour(欧拉路径)

欧拉路径是指有限有向图中，经过所有节点，但每个节点只被访问一次的路径。

欧拉路径要在欧拉图可以找到，满足欧拉图的条件：
1. 图是连通的，图上任意两点总有路径相连。
2. 下面满足两者之一就可以：
- 2.1 有且只有一个点的入度比出度少 1（作为欧拉路径的起点），有且只有一个点的入度比出度多 1（作为终点），且其余点入度=出度。
- 2.2 所有点入度=出度。
如果已知图存在欧拉路径，如何找到欧拉路径？有两个方法：
1. Fleury(佛罗莱)算法。
2. Hierholzer 算法。
Hierholzer 算法：
1. 在满足条件的欧拉图的基础上，从出发点开始出发。
2. 向任意一个点出发，把当前路径删除，将起点插入结果数组头部，把目标点定为新的起点。
3. 不断重复 2 操作，直到结束，那么输出数组就是欧拉路径了。

示例： “332. Reconstruct Itinerary” Graph C++

MST(Minimum-cost Spanning Tree 最小生成树)

从一个边带权重的联通图，生成一个联通所有结点的总权重最小的树的算法。

如果是稠密图(边数较多的图)
- 适合 Prim Naive 算法，O(V^2)
如果是稀疏图(边数较少的图)
- 适合 Prim PQ / Kruskal UF 算法，O(ElogV)

Prim PQ是最常用的方法，其他方法可以作为 follow-up

Kruskal UF可以作为通用模板使用，因为其性能较高可以适应部分稠密图，rank 也可以作为 follow-up

具体实现参考： MST

示例： “1584. Min Cost to Connect All Points” MST Golang

SCC(Strong Connected Component 强连通分量)

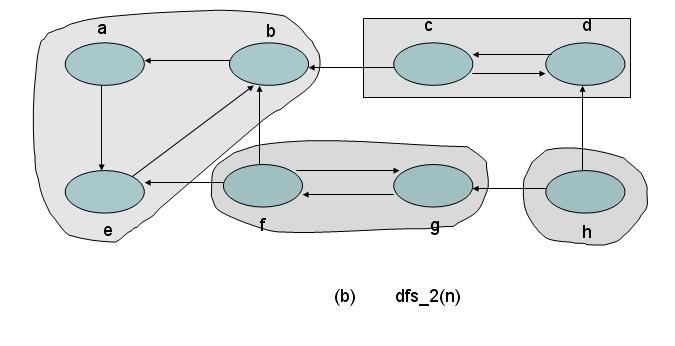
强连通图 如果在图中如果存在一条回路，使得所有结点至少被经过一次，这样的图称为强连通图。
Strong Connected Component 强联通分量 在强联通图的基础上，加上一些结点和边，使得当前的图不再强联通，称原来强连通的部分为强连通分量。单独的一个结点是一个独立的强联通分量。
求强连通图的作用：
- 在图论问题求解前，可以将强联通分量合为一个点，以简化之后的计算
- 求强联通分量的过程可以分析出环、环的长度、关键连接结点(即去掉这些点后，图将被分割)
一般用Tarjan’s Algorithm分析，步骤：
1. DFS 遍历每一个点，在点上有两个属性：DFN_i(Depth First Node)表示遍历过程的结点序号(递增)；LOW_i表示该点向前可追溯的最小时间戳(遍历序号)。
2. 用 DFS 的算法遍历结点，保证结点只被遍历一次，设置DFN_i和LOW_i，在遍历过程中用栈记录每个结点
3. 如果下个结点的DFN_next小于当前DFN_i，找到环、开启回溯模式，则LOW_i = DFN_next，在回溯过程中也要更新LOW_i
4. 逐个出栈，直到找到DFN_i == LOW_i的结点，说明找到了强联通分量的起始点，将回溯的元素记为一个强连通分量
5. 继续遍历后面未涉及的点，直到结束
时间复杂度：O(V+E)
除了 Tarjan 算法外还有其他算法，但是 Tarjan 是最简单的并且性能也高。

示例： “1192. Critical Connections in a Network” Graph

通用算法

数组排序算法

算法名称	稳定性	基本流程	时间复杂度(平均/最差)	空间复杂度	示例	适用范围
Quick Sort(快速排序)	不稳定	综合效率最高。1. 基本思路，递归+分治，每次递归将数据分为左右两边，保证左边比 pivot 小、右边比 pivot 大。2. 通过双指针跳转+循环实现一轮 pivot 调整	`O(logn)`/`O(logn)`	`O(logn)`		最常用的排序算法，综合性能最高
Bubble Sort(冒泡排序)	稳定		O(n^2)	O(1)
Bucket Sort(桶排序)	稳定	要求数值在一定范围。1. 根据情况创建 int 数组代表桶，每个桶有一定宽度。2. 遍历源数据，在对应的桶统计	O(n)	O(n)	“1833. Maximum Ice Cream Bars” “645. Set Mismatch” “164. Maximum Gap”	适合数据范围较小的情况，空间占用最大，始终保持 O(n)
Count Sort(计数排序)	稳定	要求数值在一定范围。1. 创建对应范围的 int 数组； 2. 遍历源数据，在对应的位置计数	O(n)	O(n)	“274. H-Index” “1846. Maximum Element After Decreasing and Rearranging”	数据范围较小，空间占用大，是一种特殊的(宽度为 1) Bucket Sort
Radix Sort(基数排序)	稳定	k 是数的位数，每一轮比较其中一位(个位、十位、百位)，每一轮是一次 bucket 排序，桶的数量与基数(不重复的符号)一致，桶中存放元素数组	O(kn)	O(n)	“164. Maximum Gap”	不适合有负数的情况，否则需要特殊处理
Merge Sort(归并排序)	稳定
Insert Sort(插入排序)	稳定	每次遍历一个元素，把该元素插入到前面已排序的合适位置，插入时后面的元素后移	`O(n^2)`/`O(n^2)`	`O(1)`		由于每次插入后面的元素需要向后移动，不适合数组操作，适合链表操作
Shell Sort(希尔排序)	不稳定	插入排序的改进算法。 gap=length/2；gap=gap/2；同一组内按照插入排序处理	`O(n^1.3)`/`O(n^2)`	`O(1)`		对插入排序做了改进，但是没什么应用场景
Select Sort(选择排序)	稳定	每次遍历选取最小的一个，替换到前面已排好序的最后一个	`O(n^2)`/`O(n^2)`	`O(1)`
Heap Sort(堆排序)	不稳定

KthLargest(nth_element)

“求数组中第 K 大元素”一般可以用排序、堆的办法处理，但是时间复杂度都是O(nlogn)。实际上可以借助 QuickSort 的 partition 思想将时间复杂度降为O(n)。 C++ STL 里就有这个实现：nth_element

思路：
- 首先实现 partition 函数，类似 QuickSort 的实现，但是当前指针无需在两边跳，只要遍历一遍找到中值下标即可。时间复杂度是O(n)，但实现逻辑要比 QuickSort 简单。
  - 具体步骤：
    1. 设置 pivot 为最右边值(可以用随机取数法优化)
    2. 记录一个小值下标为 l，当前下标 i，从左向右遍历
    3. 循环中，如果 nums[i] <= pivot 则交换当前位置 i 到 l，然后 l++
    4. 退出循环后，交换 l 和 r，则 l 就是 pivot 下标
- 在循环中调用 partition，按照二分查找思路，不断缩小 partition 的范围，最终找到目标下标，由于没有全部排序，所以节省了大量时间
时间复杂度：由于每次 partition 中遍历范围在快速缩小，partition调用次数 * partition内遍历范围 = n，时间复杂度是O(n)
空间复杂度：没有额外空间，O(1)

示例： “215. Kth Largest Element in an Array” Sort “面试题 17.14. Smallest K LCCI”

Brute Force(暴风 bf)

强行向前推进，最简单的算法。

例：”121. Best Time to Buy and Sell Stock”

DC(divide and conquer 分治法)

将复杂问题分解为不同子问题，然后再顺序或嵌套解决。

例：“229. Majority Element II”、“857. Minimum Cost to Hire K Workers”

DP(Dynamic Planning)

参考： Algorithm Dynamic Planning 花花酱 DP Note

Sliding Window(滑动窗口)

窗口横向长度可以动态改变，不断保持窗口内符合条件。适合子数组类题型或特定长度的字符串匹配。

例：“76. Minimum Window Substring”

Window 不一定只向后运动，Window 的右边框还可能向左运动，只要保持整体向后运动就可以。

如：“727. Minimum Window Subsequence”

Rolling Hash

Rolling Hash 是 Sliding Window 的一个变种，用HashCode的方式 Window 内的元素压缩为一个值，可以在O(n)内判断 Window 内的元素序列是否重复出现。 Rolling Hash 算法的真实名字是Rabin-Karp algorithm，主要用于子字符串匹配。

HashFunction 可以根据具体情况选择，对于字符串，可以用x*(26^k)作为 HashFunction。这里选 26 是因为小写字母共 26 个，可以根据情况调整。
Window 移动时 HashCode 计算的基本步骤：设窗口长度为k、当前下标为i
1. 窗口右移：hashCode *= 26
2. 删除尾部元素: hashCode -= nums[i-k]*(26^k)
3. 添加新元素：hashCode += nums[i]*(26^0)
要考虑Collision(Hash 碰撞)的情况，有两种方法：
1. 这时可以按顺序遍历比较一遍。只要碰撞次数足够低，算法性能就不会退化。
2. 设定一个较好的 HashFunction，避免碰撞发生。(算法题 Case 可能凑出来，实际使用无法依赖) 一般来说，我们选取一个大于字符集大小（即字符串中可能出现的字符种类的数目）的质数作为 base，再选取一个在字符串长度平方级别左右的质数作为 mod，产生哈希碰撞的概率就会很低。

示例： “1044. Longest Duplicate Substring” SlidingWindow RollingHash “1392. Longest Happy Prefix” SlidingWindow RollingHash 应用于回文“214. Shortest Palindrome” SlidingWindow RollingHash

KMP

KMP 也是 Sliding Window 的一个变种，性能达到了子串比较的极致。其特点是匹配过程中中间某个位置一旦不匹配就自动跳过一定数量的元素，避免不必要的比较。

DFS(depth first search 深度优先遍历)

深度优先遍历也叫search(搜索可能性空间)，可以用函数递归(recur)和栈(stack)实现，算法复杂度 O(n^n)或 O(n^2)。如果需要把所有可能性遍历到，选 dfs 较好，递归代码较简单。

由于算法复杂度过高，规模较大时往往可以通过记录中间结果的方法避免重复计算(这个过程叫 memo，也叫剪枝)，中间结果一般存储三个状态：默认值、有效（或具体有效值）、无效（无法找到答案）。在递归时，往往有这样两个选项，“加上当前位置、递归”、“不加当前位置、递归”，这时候“加上当前位置”要放在前面执行，这样可以尽早探索出无效路径，避免大量无用探索。例：“22. Generate Parentheses”、“386. Lexicographical Numbers”、“547. Friend Circles”

Backtracking(回溯)

是 DFS 的一个分支，用于探索某个迷宫，在过程中需要记录、恢复现场，然后尝试下一个方向。

每一级先处理”选取自己”的情况，这样可以尽早获取答案，减少无效回溯。

例：“52. N-Queens II”

有时当前位置可选项不止一种，需要在多种可能性间用循环遍历

BFS(breadth first search 广度优先遍历)

dfs 逻辑容易实现但是有些情况可能会性能很差无法通过性能测试 Case，这时要考虑用 BFS。可以用 queue、set 等进行演化。bfs 相比 dfs 可以提高性能的条件是，只要找到一个可能或最短的答案就可以，而不是要遍历整个可能性空间。如果目标方向是固定的，dfs 可以通过 visited 记录少走重复路线，dfs 实现较简单；但是如果方向是不固定的，dfs 很容易走入浪费时间的搜索空间，用 bfs 就更好。 bfs 也可以加入 visited 提高性能，一般用 bucket 或 hashtable 实现。

例：“127. Word Ladder”、“286. Walls and Gates”、“490. The Maze”

`A*` 启发式搜索算法

参考: BreadthFirstSeach A*

Bucket

核心思想是元素集合的整体范围可以分割为有限数量的”桶”，每个桶覆盖较小范围，然后通过遍历元素，利用有限的桶进行匹配、累加，以便降低遍历范围从而降低复杂度。

bucket 的算法可以用不同的数据结构实现
- vector 实现，如”923. 3Sum With Multiplicity”、”740. Delete and Earn”
- hashtable 实现，如”220. Contains Duplicate III”

Random

利用随机可以解决很多问题。

通常最基本的函数是rand()返回[0,1)之间的浮点数，如 Go 的rand.Float32()
每次使用随机前，一定要用随机值(如启动时间戳)初始化一下随机种子，如 Go 的rand.Seed(time.Now().Unix())
如果没有外界物理条件参与，计算机只能产生伪随机值，即使上面的初始化方法还是可以推测出随机序列值。真正的”随机”，往往需要从物理外界输入，比如”随机噪声”。但是应用或做题一般要求没那么严格，伪随机也够用。

Normal Random

普通随机问题，利用随机值实现一些概率问题。

实例： “470. Implement Rand10() Using Rand7()” Random Normal 1 2 “380. Insert Delete GetRandom O(1)”

Rejection Sampling(拒绝采样)

利用暴力求解，多次生成随机值，只选取符合条件的采样，只要时间复杂度合理即可。

这种算法往往用于暴力模拟某种物理问题

实例： “470. Implement Rand10() Using Rand7()” Random Rejection Sampling “478. Generate Random Point in a Circle” Random

Reservoir Sampling(蓄水池抽样)

可以从流式数据中抽取样本，在N个已知样本中抽取K个(N>K)，并且每个样本被抽取的概率都为K/N

具体推导过程参考： Reservoir Sampling

实例： “398. Random Pick Index” Random “382. Linked List Random Node” Random

Random Pick with Weight(带权重的随机选择)

对于离散的元素，可以放入数组，利用数组中相同的元素的数量来增加元素的命中概率

示例： “380. Insert Delete GetRandom O(1)” StructDesign “381. Insert Delete GetRandom O(1) - Duplicates allowed” StructDesign

可以利用前缀和(preSum)，生成一个概率映射数组，然后每次随机时利用二分查找取得结果元素

示例： “528. Random Pick with Weight” Random “497. Random Point in Non-overlapping Rectangles” Random

Fisher-Yates Algorithm(Fisher-Yates Shuffle 洗牌)

Fisher-Yates 是最优洗牌算法，利用数组的原位置进行洗牌，并保证每个元素在每个位置的概率相同。只遍历一遍，时间复杂度 O(n)

步骤：
1. 遍历每个元素位置
2. 每个位置时随机取一个目前剩下元素数量的随机整数，随机数作为元素下标，与当前位置的元素相交换
3. 遍历完毕、洗牌结束

示例： “384. Shuffle an Array” Random Golang

KNN algorithm（Kth Nearest Neighbor）

KNN 是一种最典型的分类算法，

一般步骤：
1. 数据标准化处理，各个维度的数据转为同一数量级（两种常用方法：线性归一化 Min-Max scaling、0 均值标准化 Z-score standardization）。
2. 通过新值与样本的距离（欧氏距离/曼哈顿距离/余弦定理）取得最近的 K 个邻居。
3. 由 K 个邻居的类型投票决定，K 的取值最好为 3~10 之间的奇数。
4. 通过实验观察，调整 K 的值到最优。

例：”973. K Closest Points to Origin”

Minimax

Minimax（极大极小值搜索，博弈论 Game Theory）,对弈双方都希望让自己 max 而让对方 min，假设双方都有全部信息、不能存在随机动作、能够预测全部未来，那么最终博弈结果一般是某方赢或平局。按照游戏规则，利用 DFS 的方式搜索整个可能性空间，逐步演化出最终的结果。

组合游戏的形式有两种，我们研究的范围是ICG(Impartial Combinatorial Games)，在游戏中两个玩家所能进行的移动是完全相同的。另一种形式 Partizan Combinatorial Games，是指两个玩家分别有不同的移动，比如象棋。

Minimax 可以有两种解法：DFS+memory和DP。用 DFS 的方式更直观，可以按照模板，修改递推公式就可以；DP 需要考虑转移方程和迭代方向，总代码量会更少。

例： “486. Predict the Winner” “877. Stone Game” “913. Cat and Mouse” “1025. Divisor Game” “1140. Stone Game II” “1406. Stone Game III” “1510. Stone Game IV”

Line Sweep(扫描线)

思路：如果在时间或空间轴上有多个元素，每个元素的开始和结束都分别会影响最终结果，这时不要尝试遍历元素，而是要将元素的影响点拆解、排序，然后按顺序遍历每个影响点求得结果。

由于存在排序，基本时间复杂度 O(nlogn)

示例： “56. Merge Intervals” “57. Insert Interval” “252. Meeting Rooms” “253. Meeting Rooms II”

对于有多个属性的情况，要注意排序时候要正确处理不同属性的优先级

示例： “1288. Remove Covered Intervals”

对于多个属性的情况，可以利用 PriorityQueue(Heap) 维护扫描线上的元素

示例： “218. The Skyline Problem” LineSweep Golang

一般 LineSweep 可以先出一个简易逻辑(代码多)，然后再进一步优化为核心逻辑(代码少)，一般优化只涉及存储优化，时间复杂度相同

示例： “986. Interval List Intersections” LineSweep Golang

Boyer-Moore(摩尔投票法) 可以解决 Majority-Element(众数问题)

问题：在一个元素数组中，找出大于某一比例(如 1/2)的元素，要求时间复杂度O(n)，空间复杂度O(1)
步骤：算法基本思路就是”小弟够多不怕对砍”
1. 对某个元素进行计数，如果遇到这个元素则计数加一;
2. 如果不是这个元素则计数减一；如果为零则重新更换当前计数元素。
3. 最后如果计数大于 1，则遍历数组对找到的元素计数，如果总数超过了 1/2，则找到了目标。
要点：
- 处于当前计数的元素数与目标比例有关，元素数 = 分母数 - 1，上面目标比例为 1/2 则只需要统计 1 个元素
- 遍历统计时，只要其中一个元素可以累加/初始化(count 0->1)，则 continue
- 如果无法累加/初始化，则两个元素计数都要减

实例： “169. Majority Element” Array “229. Majority Element II” Array

Skill

剪枝

在做某种可能性空间搜索时，如果某一状态以前已经遍历过，可以直接取得这个状态的结果，避免重复计算。这就好像遍历树的时候，对一些已知肯定没有结果的支杈进行剪枝一样。通常可以用 map 把状态结果保存，可以快速判断和返回。

inplace(原地)思想

利用数组位置有时题目给定的数组元素只需要遍历一遍，这时可以利用原数组位置存储遍历结果以便后面使用。这样可以节省空间，对逻辑也没有干扰。
- 示例： “448. Find All Numbers Disappeared in an Array” “645. Set Mismatch”
利用 bit 位有时题目给定的数组元素有效位并不多，比如元素是 int32 型而表示的数范围是 1byte 内，那么实际上有将近 3byte 是可以利用的空间，可以存储一些中间结果。
- 好处：
  1. 减少空间复杂度，直接利用原有输入参数的空间
  2. 不需要考虑映射关系，直接在原地操作即可
- 坏处：
  1. 如果原数据和新数据边界不好划定，容易出错
利用原链表结点有时做链表处理时，题目会要求不允许新建/修改链表结点，要利用原链表结点操作

对于存储容量较大的迷宫题，为了节省容量，可以利用原有二维数组元素的高位存储中间值，通过二进制操作在原位置保存更多信息并读取原值。

如：”289. Game of Life”。

对于给定容量非常有限(空间复杂度 O(1))的情况，也可以用这种思路。虽然没有用位操作，但是利用负数存储原有正数值和访问过的叠加状态。

如：”41. First Missing Positive”

状态压缩

有时需要一个整型数组或结构体保存一个状态信息，状态较多时会占用很多容量。可以用二进制思维，将可独立的状态标识用一个 bit 表示。这样一个综合的状态可以表示为一个 int，或者 bool 数组，相比整型数组或结构体要节省一两个数量级的容量。

如：”847. Shortest Path Visiting All Nodes”

常数内尝试

有时可以利用题目条件中某个参数数量有限，可以穷举所有该参数也不会影响时间复杂度，这时可用这种思路解决。

示例：穷举所有不同字母数量。 “395. Longest Substring with At Least K Repeating Characters” SlidingWindow Golang

固定方向检测

比如 8 方向、4 方向、2 方向等，可以将对应方向的执行参数写入数组，然后循环执行，通过计数对数组容量取余来切换方向。

例：[“489. Robot Room Cleaner"]()

未知方向结果记录(左右或上下左右)

未知方向结果记录(左右或上下左右)，可以用 map 记录结果，也可以使用多个 vector 记录不同方向。

使用 vector 性能会更高，

如：”314. Binary Tree Vertical Order Traversal”。

使用 map 会更方便，

如：”489. Robot Room Cleaner"。

P(Polynomial) 问题

如果计算的数列、数值符合某种公式(P 问题)，可以先推导出等价公式，然后用暴力方法计算结果，注意计算是要保证被除数能够被整除。

如：”621. Task Scheduler”、”829. Consecutive Numbers Sum”

自然数 bucket

如果处理的数组是不重复自然数或整数，并且取值范围也是 N 以内，那么可以用该自然数和数组下标的对应关系进行 swap 处理（时间复杂度 O(n)），排序、查重等计算。

如：”41. First Missing Positive”

每 3 个元素之间有关系时

可以使用 hashmap 快速找到关联元素例。

如：”1. Two Sum”、”446. Arithmetic Slices II - Subsequence”(阿里巴巴)、”560. Subarray Sum Equals K”。

(C++)nth_element 函数

对于只需前 K 个元素排序、后边元素比前 K 个都大、可乱序的情况，非常适合 nth_element 函数(时间复杂度 O(n))。

例如：”324. Wiggle Sort II”、”973. K Closest Points to Origin”。

bitmap

如果要检查的元素集很有限，可以利用二进制操作生成 uint32 bitmap 进行存储，然后用 unordered_map 存储，这样节省容量、运算效率高。

例：”187. Repeated DNA Sequences”

多个属性用 map 或 set 排序

如果多个属性用有序 map 或 set 排序，实现比较函数比较麻烦，可以将不同属性使用不同位的数值，优先级高的在高位。

如：“460. LFU Cache” Design Golang

排序和函数调用的时间顺序有关

有些情况，排序和函数调用的时间顺序有关，可以用一个变量做持续自增运算，适时的使用。如：”460. LFU Cache”

嵌套表达式 Parse 类的题

逻辑简单有效的方式就是通过一个引用类型的 pos 顺序向前或向后一直 parse，通过递归函数解决嵌套问题，通过不同类型处理函数分治局部类型，局部作用域变量通过 map 存储，涉及字符串拼接可以用strings.Builder。

例：”394. Decode String”、”726. Number of Atoms”、”736. Parse Lisp Expression”

“并发资源占用”问题

用有序 map 进行时间轴模拟最 concise。如果没有 map，可以分别将开始和结束时间点存入数组，然后排序，再按照顺序遍历。

如：”253. Meeting Rooms II”

设定 DP 演化边界条件

某些情况下，题目设定的参数规模之间是冲突的，这时要选取对结果有影响的最小范围进行迭代

如：”1269. Number of Ways to Stay in the Same Place After Some Steps”

Discretization 离散化处理

有些情况下，给定的数组不能符合算法需要的前提条件，这时可以利用 Discretization 重整为符合条件的数组，比如：
1. 元素太稀疏，无法用 bucket/DSU/BIT/ST 算法
2. 元素包含负数，而目标算法只能用于正整数
3. 元素种类不同，我们只关心元素顺序关系而不关心元素值，想把顺序关系简化
Discretization 步骤：
1. clone 原数组，对新数组进行排序，得到有序数组
2. 准备一个 HashMap，key 是元素值、value 第一次加入该元素时 HashMap 的容量。遍历有序数组，构建 HashMap。HashMap 的 value 值，就是原不重复元素的 紧密排列
3. 再次按逻辑遍历原数组时，可以直接利用 HashMap 找到其在不重复元素中的序号(从 0 开始)
示例：
1. 元素稀疏：”315. Count of Smaller Numbers After Self”
2. 元素有负值：”315. Count of Smaller Numbers After Self” 这种情况也可以用整体加一个偏移量，使得最小负数转为正整数解决

Little Tips

数组中间元素下标

设数组的长度为 n，如果 n 为奇数，则中间元素下标是n/2，经过整数向下取整，正好为中间下标；n 为偶数，则中间下标是(n/2)-1。

可以用统一公式(n-1)/2表示中间位置。

乘/除 2

用x>>1代替x /= 2可以节省 CPU 周期提高效率

判断奇偶性

用x & 1 == 1代替x % 2 != 0。因为位操作 CPU 效率远远大于取模。

负数取余

为了让负数的取余结果也落在[0,n)范围内，可以((x%n)+n)%n

Golang Tips

LeetCode 可以用fmt输出调试，无法用log输出
Golang 中缺少一些常用的常量定义，可以自己用位操作实现
- const UINT_MIN uint = 0 // 所有位都是 0
- const UINT_MAX = ^uint(0) // 所有位都是 1
- const INT_MAX = int(^uint(0) >> 1) // 第一位是 0，其余都是 1
- const INT_MIN = ^INT_MAX // 第一位是 1，其余都是 0

可以自己实现常用的 swap 函数

func swap(a, b *[]int)  {
	*a, *b = *b, *a
}

自己实现 max/min 函数

func max(a, b int) int {
  if a > b {  // 注意这里不用 >= 符号，没有必要
     return a
  }
  return b
}
func max(sli ...int) (ret int) {
  ret = math.MinInt32
  for _, n := range sli {
      if n > ret {
          ret = n
      }
  }
  return ret
}

自己实现 set 一般用 map[int]struct{} 可以实现 set，但有时为了快速判断是否存在节省代码，可以用 map[int]bool

C++ Tips

C++语言特性

有时可通过类内重命名，避免重复定义代码。”typedef std::unordered_map<std::string,std::string> stringmap;”
C++11 新特性：对于空指针，使用 C++11 的 nullptr 更好。执行 delete nullptr 时，什么都不会做。所以 delete 的指针要及时设置 nullptr。
跨函数的变量，可以考虑用类的成员变量的方式传递，比传参更符合面向对象设计。
在对 map 元素操作时，可以直接对未知元素进行自增、自减运算，map[x]–，如果该空间不存在，自动创建时值默认为 0。
如果没有必要对统计计数，可以用 unordered_set 代替 unordered_map 以节省容量。
如果想实现一个较大距离的位操作，可以用 bool[n]实现。
使用 hash 函数时一定要搞懂具体函数原理，可能会发生排序与 hash 结果无关的情况，导致重复。
可以利用 map 的有序搜索二叉树原理，lower_bound 查找最小 key 值以及对应的 value。在构造 map 时使用 greater就可以查找较大值。
C++中的封装类 string，其实本质还是 char*，s[s.length()] == ‘\0’ 并不会越界。
数组作为参数传递时，第一维的长度是不重要的，可以空着，相当于传数组的引用。如：bool flags[][9][9]
C++14 新特性，返回任何空容器”return {};”，不需要构造一个空容器再返回。在调用 push_back 等函数时，如果是 pair 等集合类型，可以直接用”{v1,v2}”代替构造函数传入 push_back。注意，必须在上下文完全确定类型的时候才能使用，不是任何地方都能使用。
C++11 新关键字”decltype(value)”，宏函数以变量类型替换位置。
C++11 新特性，在类的拷贝构造函数、赋值构造函数后加”= delete;”，”SegmentNode (const SegmentNode &) = delete;”表示禁止生成对应的默认构造函数，这里函数只要参数类型不要参数名称，因为不会有具体实现。对应的加上”= default;”表示生成默认的构造函数。以前是需要自己都创建一下表示考虑到了，现在有这两个语法也是相同的作用。
“for (auto p : dict)”一般这里的 p 都是引用类型，可直接进行赋值等操作。
查找容器中是否存在时，使用 count(value)比 find 会精炼一些。
C++中想跳出多重循环，有两种方法：1 使用 goto 语句”targetLine:\n goto targetLine;”。2 在外层循环添加判断条件变量，在内层用 break。
C++中运算符的耗时情况’/’ = ‘%’ » ‘+’ = ‘-‘ = ‘*’ » ‘»’ = ‘=’。数量级对比：’/’ ≈ 1000; ‘+’ ≈ 50; ‘=’ ≈ 1;
double 溢出后不会直接抛出异常，而是保持最大值不再变化。
在进行 for 循环时，如果涉及到字符串长度与下标比较的情况，不要使用”i < str.size() - 2”这种形式，应该用”i + 2 < str.size()”，因为 size()函数返回的是 size_t 类型是 uint32 类型的，如果 size()返回的是 0，”0-2”就会被看做一个超大的 uint32 数，就可能造成无限循环。还可以在函数一开始就计算一个 int N = str.size()，这样后面使用”i < N - 2”就不会出问题了。
vector::back()、stack::top()等函数，返回的是引用，可以直接修改值。
map<pair<int,int>,int>正常编译，而 unordered_map<pair<int,int>,int>会无法编译，大概因为 unordered 无法支持复杂结构的 hash。
queue、priority_queue、stack 没有赋值构造函数，只能逐步构造。大概是因为这些结构没有迭代器，无法进行批量元素拷贝。同样的，这类数据结构也没有 clear 函数，不能直接清空。

C++基本语法

new 数组：int* pVisited = new int[num]; delete 数组：delete[] pVisited;
在 C++中“乘方”应该用函数 pow(x,y)实现(包含 math.h)，而’^’符号是异或运算。
C++类中，类型声明要有顺序关系。所以，做题时，一般声明都要放在前面，定义要放在声明之后。一般顺序是：私有声明、私有定义、公有声明、公有定义。
’.’ 、’&’、’!=’ 符号顺序要注意括号，避免逻辑错误。按位操作的优先级要低于比较操作符，例如”M[x][y]&0b10 == 0”，”0b10 == 0”会被优先运算。
子类调用父类同名函数或变量”ClassName::FunctionName()”;
λ 表达式(匿名函数)：返回类型自动判断，使用 auto 类型时，λ 函数不需要标明返回值类型。λ 表达式可以直接替代 Compare 对象。auto add= { return a + b; }; int (*add)(int a, int b) = ->int{ return a + b; };
二进制表示”0b101”,十六进制”0xaf”，八进制”017”。
double 型表示科学计数法，”2.3e14.3” => “2.314.3”
C++中强制转换一般为”double(x)”，而 C 中一般为”(double)x”，尽量使用 C++的方式。
成员函数声明时右边加 const 表示该成员函数不会改变任何类内变量。

计算机基本原理

ascii 的范围是 0~127，一共是 128 个字符。
对于可能 int32 溢出的情况，可以在运算时使用 long long 类型，避免溢出。
从 C 语言继承来，在常量数字后面可以加上类型符号，避免被自动转换。如：10LL、10UL、10u、0.3f。例如：1000000000000 已经超过了 int 范围，long a = 100000000000000;在有些编译器会出错，写成 100000000000LL 就不会有问题了。

名词表

sum 和，多个数相加的结果
product 乘积，多个数相乘的结果
factor 因子，参与乘积的因数
prime number 质数/素数。不可以被除 1 外的数整除的数。规定 1 是质数。
prime factor 质因数。将一个数分解成多个因数相乘的形式，如果其中的因数无法再分解(是质数)，则称之为质因数。
square 平方，x^2 == x * x
square root 平方根，平方的逆运算
cube 立方，x^3 == x * x * x
cube root 立方根，立方的逆运算
等差数列 一个数列紧邻两元素之间的差为固定值，如1,3,5,7，这时公差为 2
等比数列 一个数列紧邻两元素之间的商为固定值

基本概念

做题流程

其他技巧

C++ 技巧

Golang 技巧

数据结构

Array(数组)

多维数组

算法：BinarySearch(二分查找)

LowerBound

UpperBound

环状 array 技巧

前缀和压缩(prefix sum)

差分(diff array)

Kadane 算法(最大连续字段和)

Heap(堆)

LinkedList(链表)

算法：归并排序

算法：快慢指针法(Tortoise and Hare)

技巧：添加辅助头节点

链表相交点

利用相邻结点保存关联关系

DFS 处理每个结点

Stack(栈)

算法：Monotone Stack(单调栈)

stack 背影法

多个栈配合

Queue(队列)

DQueue(double queue，双向队列、双端队列)

算法：Monotone Queue(单调队列)

Priority Queue(PQ)

Heap(堆)

Heap 延迟删除

Tree(树)

Binary Tree（二叉树）

BST(Binary Search Tree 二叉搜索树)

Balanced BinaryTree(平衡二叉树)

Treap(Tree Heap 树堆)

TrieTree(Prefix Tree 前缀树)

BinaryIndexTree(索引树)

ST(SegmentTree 线段树)

Red Black Tree (红黑树)

HashTable

Longest Consecutive Sequence (最长连续子串)

结合 Array 实现 O(1)容器

Ordered Map(有序 Map)

Graph(图)

最短路径

Dijkstra(狄杰斯特拉)

Bellman-Ford

Floyd-Warshall

Topological Order(拓扑排序)

DSU（Disjoint Set Union 并查集 ）

Euler tour(欧拉路径)

MST(Minimum-cost Spanning Tree 最小生成树)

SCC(Strong Connected Component 强连通分量)

通用算法

数组排序算法

KthLargest(nth_element)

Brute Force(暴风 bf)

DC(divide and conquer 分治法)

DP(Dynamic Planning)

Sliding Window(滑动窗口)

Rolling Hash

KMP

DFS(depth first search 深度优先遍历)

Backtracking(回溯)

BFS(breadth first search 广度优先遍历)

A* 启发式搜索算法

Bucket

Random

Normal Random

Rejection Sampling(拒绝采样)

Reservoir Sampling(蓄水池抽样)

Random Pick with Weight(带权重的随机选择)

Fisher-Yates Algorithm(Fisher-Yates Shuffle 洗牌)

KNN algorithm（Kth Nearest Neighbor）

Minimax

Line Sweep(扫描线)

Boyer-Moore(摩尔投票法) 可以解决 Majority-Element(众数问题)

DSU（Disjoint Set Union 并查集）

`A*` 启发式搜索算法