Redis HyperLogLog Data Structure

Posted on

Peano HyperLogLog 算法是”大数据的基石”之一，可以做基数概要估算，即统计不重复的元素大概个数。适合统计数量巨大但无需知道具体元素的场景，存储 2^64 个不同元素的统计值，只需要 12KB 内存，标准差 0.81%。本文记录 HyperLogLog 的算法演化思路及 Redis 实现的数据结构。

一般统计元素的思路

  1. Set 每个元素加入 set，最后统计 set 的总数。这种统计较为精确，但是容量太大。

  2. Bitmap 用一个 bit 位来表示一个元素。相比 Set 更节省容量，但是在元素较多时同样会占用太大容量

伯努利试验

伯努利试验是概率论中的内容，设硬币有正反两面，一次上抛后落下，出现正面或反面的概率都是 50%。假设一直抛硬币，直到出现正面为止，就记录为一次伯努利试验。

对于多次的伯努利试验，假设次数为n，则意味着出现了n次正面。设每次抛掷了k次才看到正面，第一次伯努利试验对应的抛掷次数为k1，依次类似，第n次对应的抛掷次数为kn。对于这n次伯努利试验中，必然有一个最大的抛掷次数，我们记为k_max。

结合最大似然估算方法，存在估算关联：n = 2 ^ k_max，用这种方法就可以通过k_max反推出n。

LogLog 算法

如果只做一次伯努利试验，上面从k_max反推到n存在较大的误差，有可能第一次就抛掷很多次才看到正面。如果增加伯努利试验的次数，当n足够大时候可以减少误差。还可以将多次试验作为一轮，测试多轮后取k_max的平均值，再计算n值，这就是LogLog算法:

\[DV_{ll} = const \cdot m \cdot 2^{\bar R}\]
  • \(DV_{ll}\)对应n
  • const是修正因子，根据不同的n取值不同
  • m是伯努利试验的轮数，每轮包含多次试验
  • \(\bar R\)表示k_max的平均数(k_max_1 + ... + k_max_m)/m

HyperLogLog

与 LogLog 算法相比HyperLogLog算法把平均数改为了调和平均数，减少了偶现的大数值的影响。

\[DV_{HLL} = const \cdot m \cdot {\frac{m}{\displaystyle \sum_{j=1}^{m} \frac{1}{2^{R_j}}}}\]
  • Mean Value(平均数) 各元素 x 求和后除以元素数量 \(\bar M_n = \frac{\displaystyle \sum_{i=1}^nx_i}{n}\)
  • Harmonic Mean(调和平均数) x 的倒数，的平均数，再取倒数 \(\bar H_n = \frac{1}{\frac{1}{n} \displaystyle \sum_{i=1}^n \frac{1}{x_i}} = \frac{n}{\displaystyle \sum_{i=1}^n \frac{1}{x_i}}\)
  • 与平均数相比，调和平均数将较大的值的影响减小了(小于 1 的值放大了)
  • 标准差(Standard Deviation)公式为\(SD=\frac{1.04}{\sqrt m}\)，所以 m 越大偏差越小

Redis 对 HyperLogLog 的实现

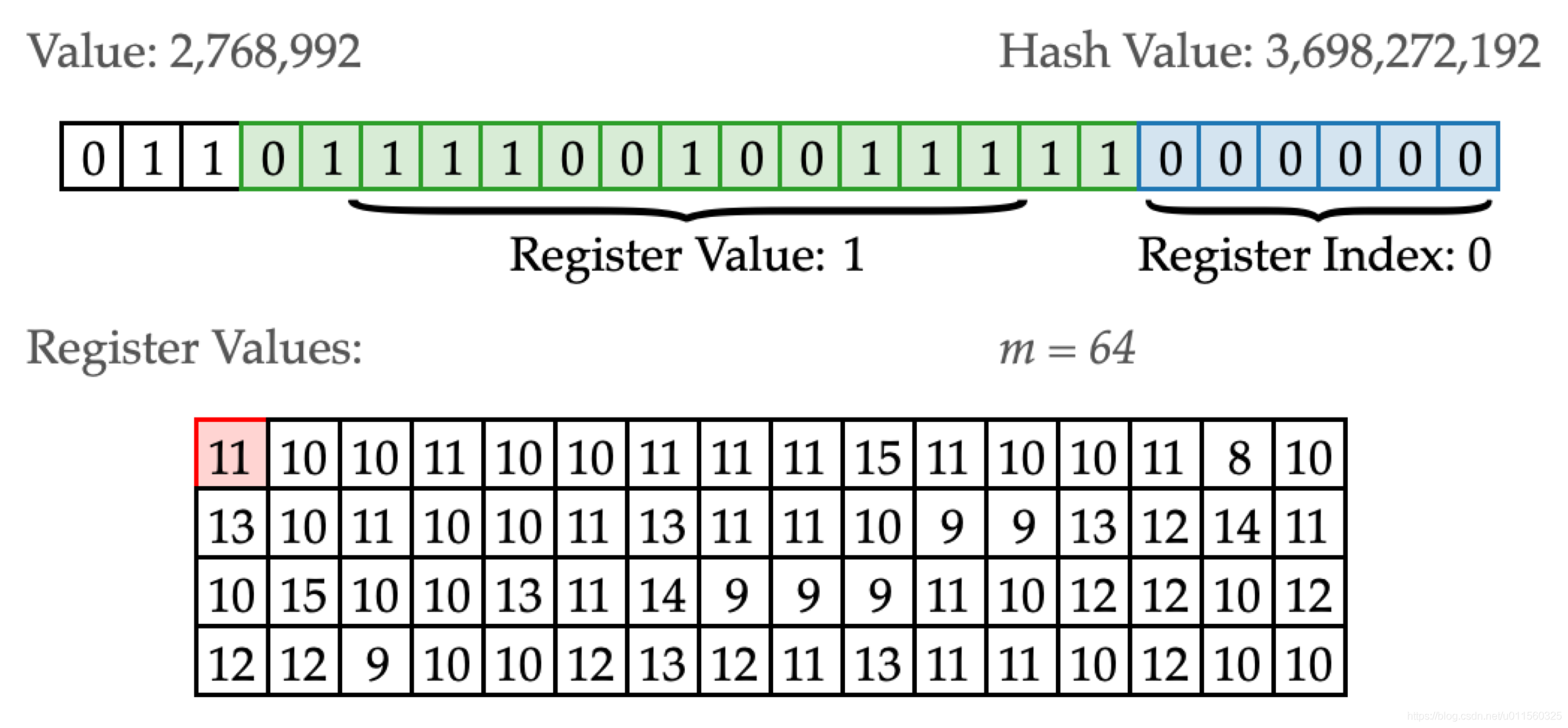
  1. Hash 为比特串 拿到一个元素后，先通过Hash函数计算出一个64位的输出值。其中0表示反面、1表示正面，例如1001000，这样从低到高(从右向左)可以看作一次伯努利试验的多次投掷，即k_max = 4(第四位出现了正面)
  2. 分桶 这里的桶对应前面说到的轮，即通过增加桶(轮)数来降低误差。我们取比特串前(最低的)14位作为桶的数量，对应值为16384 = 2^14。剩下的50位来计算一次k_max，用6位可以表示(2^6 = 64 > 50)。所以一共需要的内存容量为12KB = 98304 bit = 6 * 16384。 例如：一个 Hash 后的值...0100...00100，桶值为...000100十进制对应 4，k_max值为...010。则找到第 4 个桶，比较桶内原值和 2(2 = b10 = 2^0 + 2^1)的关系，如果小于 2，则设置桶内值为 2
  3. 统计 取n时，可以按照HyperLogLog的算法对所有桶值做统计
  • HyperLogLog 的底层其实是一个非常大的 Bitmap，或者说多个连续的 Bitmap 串成的
  • 虽然一个 HyperLogLog 对象存储只占 12KB，但是 Redis 为了避免稀疏值(大量 0 值)导致内存浪费，将存储分为”密集存储”和”稀疏存储”
    • 密集存储就是连续 16384 个 6bit 的串成的位图，其中每个 6bit 是由 00 开头的一个字节的桶
    • 稀疏存储是通过记录连续 0 值的桶的数量，节省实际内存使用
    • 当某个桶的计数超过 32(达到 33)时，或总的存储超过 3000 字节，则稀疏存储会转化为密集存储
  • HyperLogLog 和 Bitmap/Set 类似，可以进行统计合并，只要把所有桶合并即可
  • 由于每个输入值的 Hash 值不同，同一个值多次输入不会影响结果，这也是基数的含义
  • HyperLogLog 中的命令以PF作为前缀，是为了致敬算法界的前辈Philippe Flajolet(2011 年去世)，著有《算法分析导论》