算法学习，极限数据结构之——跳跃表(Skip List)

Posted on

数据结构特性

Skip List 跳跃表，Skip List

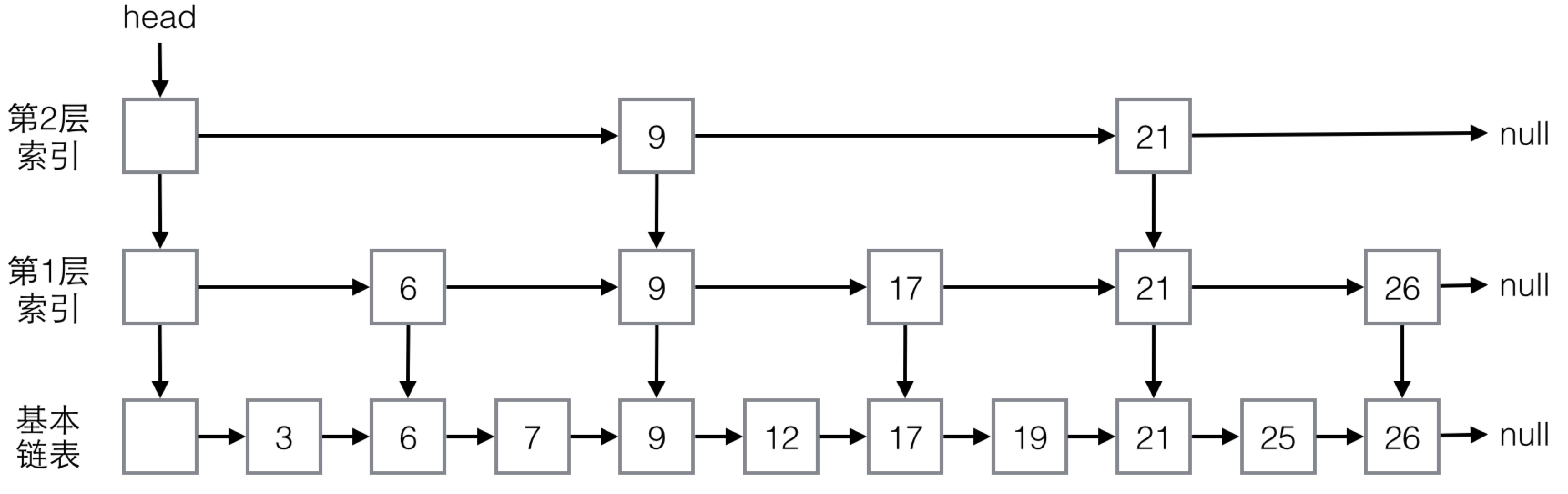
  • 由多层结构组成，每一层是一个有序的链表
  • 最底层的链表包含所有元素
  • 每个节点包含两个指针，一个下一个元素、一个下一层元素，如果在上层链表出现了那在下层也会出现

这么不起眼的数据结构，却有着红黑树和 AVL 树的性能(增删改查 O(logn)，空间 O(n))、被 Redis 采用作为 ZSet 的底层数据结构，到底是如何实现的？关键是它的插入算法——利用正态分布。

当插入新的节点时，用抛硬币(随机函数)来决定是否增加层数，而这样的结果是节点所属层数正好符合 正态分布，期望值是 2 。

与红黑树和 AVL 树相比，逻辑简单、没有复杂的旋转平衡操作，可以很容易地用链表实现。

数据结构的实现

package skiplist

import (
	"fmt"
	"math"
	"math/rand"
)

const MaxLevel = 10

// SkipElement is the element for Skiplist
type SkipElement struct {
	Value interface{}
	seq   int
	pre   *SkipElement
	next  *SkipElement
	down  *SkipElement
	list  *SkipList
}

// Prev return previous element
func (p *SkipElement) Prev() *SkipElement {
	return p.pre
}

// Next return next element
func (p *SkipElement) Next() *SkipElement {
	return p.next
}

// SkipList is a multilevel list. All operate time complexty is O(logn)
type SkipList struct {
	lists  []*SkipElement
	rend   *SkipElement
	end    *SkipElement
	length int
}

// NewList create a SkipList and return the pointer
func NewList() *SkipList {
	begin := &SkipElement{
		seq: math.MinInt32,
	}
	begin.next = &SkipElement{
		seq: math.MaxInt32,
		pre: begin,
	}
	res := &SkipList{
		lists: []*SkipElement{
			begin,
		},
	}
	res.rend = begin
	res.end = begin.next
	return res
}

// Len return the lenth
func (p *SkipList) Len() int {
	return p.length
}

// Begin return the first iterator
func (p *SkipList) Begin() *SkipElement {
	if p.rend.next != p.end {
		return p.rend.next
	}
	return p.end
}

// RBegin return the last iterator
func (p *SkipList) RBegin() *SkipElement {
	if p.rend.next != p.end {
		return p.end.pre
	}
	return p.rend
}

// End return the last iterator
func (p *SkipList) End() *SkipElement {
	return p.end
}

// REnd return the rend iterator
func (p *SkipList) REnd() *SkipElement {
	return p.rend
}

// Add or update value of a key
func (p *SkipList) Add(key int, val interface{}) (e *SkipElement, isNew bool) {
	level := 0
	// get insert level by random
	for level < MaxLevel && (rand.Int() & 1) == 1 {
		level++
	}

	for pre := p.lists[0]; len(p.lists) <= level; p.lists = append(p.lists, pre) {
		pre = &SkipElement{
			seq:  math.MinInt32,
			down: pre,
		}
	}

	var upNode *SkipElement
	for curLevel, curNode := level, p.lists[level]; curLevel >= 0 &&
		curNode != nil; curLevel, curNode = curLevel-1, curNode.down {

		for curNode.next != nil && curNode.next.seq < key {
			curNode = curNode.next
		}

		// already exists, update value
		if curNode.next != nil && curNode.next.seq == key {
			for tempNode := curNode.next; tempNode != nil; tempNode = tempNode.down {
				tempNode.Value = val
				e = tempNode
			}
			return
		}

		newNode := &SkipElement{
			seq:   key,
			Value: val,
			pre:   curNode,
			next:  curNode.next,
		}

		if upNode != nil {
			upNode.down = newNode
		}

		if curLevel == 0 {
			curNode.next.pre = newNode
			p.length++

			// set return value
			e = newNode
			isNew = true
		}

		curNode.next = newNode
		upNode = newNode
	}
	return
}

// Find the element, if not found return nil
func (p *SkipList) Find(key int) (res *SkipElement) {
	for curLevel, curNode := len(p.lists)-1, p.lists[len(p.lists)-1]; curLevel >= 0 &&
		curNode != nil; curLevel, curNode = curLevel-1, curNode.down {
		for curNode.next != nil && curNode.next.seq <= key {
			curNode = curNode.next
		}

		if curNode.seq == key {
			res = curNode
			return
		}
	}
	return
}

// Remove the element
func (p *SkipList) Remove(key int) (exists bool) {
	for curLevel, curNode := len(p.lists)-1, p.lists[len(p.lists)-1]; curLevel >= 0 &&
		curNode != nil; curLevel, curNode = curLevel-1, curNode.down {
		for curNode.next != nil && curNode.next.seq < key {
			curNode = curNode.next
		}

		if curNode.next != nil && curNode.next.seq == key {
			curNode.next = curNode.next.next
			if curLevel == 0 {
				curNode.next.pre = curNode
				exists = true
				p.length--
			}
		}
	}
	return
}

// Print out the list structure
func (p *SkipList) Print() {
	for curLevel, curNode := len(p.lists)-1, p.lists[len(p.lists)-1]; curLevel >= 0 &&
		curNode != nil; {
		fmt.Printf("level %v : ", curLevel)
		for curNode != nil {
			fmt.Printf("%v ", curNode.seq)
			curNode = curNode.next
		}
		fmt.Println()
		curLevel--
		if curLevel >= 0 {
			curNode = p.lists[curLevel]
		}
	}
}

应用示例

Challenge:
In an exam room, there are N seats in a single row, numbered 0, 1, 2, ..., N-1.

When a student enters the room, they must sit in the seat that maximizes the distance
to the closest person.  If there are multiple such seats, they sit in the seat with the lowest number.
(Also, if no one is in the room, then the student sits at seat number 0.)

Return a class ExamRoom(int N) that exposes two functions: ExamRoom.
seat() returning an int representing what seat the student sat in, and ExamRoom.
leave(int p) representing that the student in seat number p now leaves the room.
It is guaranteed that any calls to ExamRoom.leave(p) have a student sitting in seat p.

type ExamRoom struct {
    size int
    list *SkipList
}

func Constructor(N int) ExamRoom {
    return ExamRoom{
        size: N,
        list: NewList(),
    }
}

func (this *ExamRoom) Seat() int {
    res := 0

    if this.list.Len() != 0 {
        maxLen := 0 // max lenth between two seats

        if this.list.Find(0) == nil {
            maxLen = this.list.Begin().Value.(int)
        }

        for index, element := 0, this.list.Begin(); element != this.list.End();
        element, index = element.Next(), element.Value.(int) {
            if tempLen := (element.Value.(int) - index) / 2; tempLen > maxLen {
                maxLen = tempLen
                res = (element.Value.(int) + index) / 2
            }
        }

        if this.list.Find(this.size - 1) == nil {
            tempLen := this.size - 1 - this.list.RBegin().Value.(int)
            if tempLen > maxLen {
                maxLen = tempLen
                res = this.size - 1
            }
        }
    }

    this.list.Add(res, res)
    return res
}

func (this *ExamRoom) Leave(p int)  {
    this.list.Remove(p)
}

复杂度推导

决定插入节点所属层数的代码：

1
2
3
4
level := 1	// 为了便于说明，初始值设为1，表示1层
for (rand.Int() & 1) == 1 {
	level++
}

※在实际的 Redis 源码中，深度最大值为 64，可以支持 2^64 个元素。没必要无限的增长，反而会降低效率。

插入 n 个 key 后，每一层的节点数期望：

  • 第 1 层 n，任何节点至少要插入第一层
  • 第 2 层 n/2，只要第一次发生随机增 1 的，都要有第 2 层
  • 第 3 层 n/4
  • …
\[E(节点数) = n\sum\limits_{i = 0}^\infty {\frac{1}{2^i}}\] \[\Rightarrow n\cdot(1 + \frac12 + \frac14 + \frac18 + \cdots) = n\cdot2\]

空间复杂度为 O(n)

类似的，因为链表的结构符合正态分布，增、删、改、查一次的时间复杂度为 O(logn)