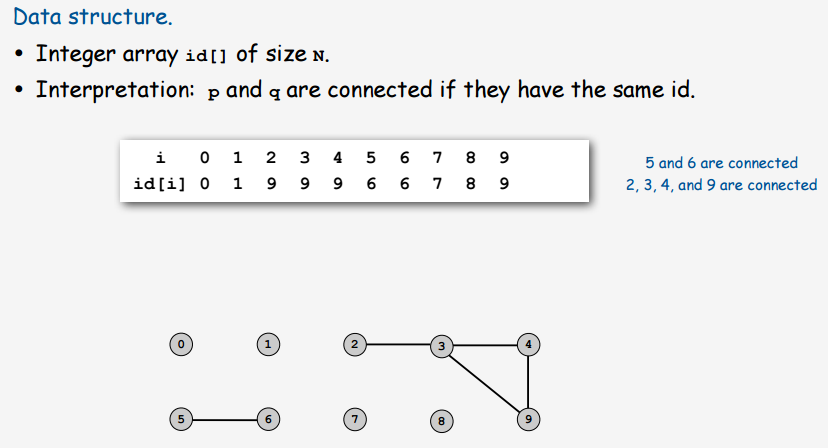
数据结构特性

并查集，DSU(Disjoint Set Union)，对应的算法也叫 Union Find。
该数据结构用于将有关联的元素合并为多个集合，使用非常简单、实现逻辑也不复杂。
对数据进行紧密排列处理(将离散数据紧密排列后添加 id)后空间复杂度 O(n)，时间复杂度 O(n)，性能非常好。

有些情况下，元素并不是紧密排列的，而是比较稀疏的，比如[0~1e9]之内的 1000 个元素。这时需要利用”Array+hashMap”的方式对元素进行”重排”，变为排列紧密的数据后，再利用 DSU 处理

数据结构的实现

// C++版本
class DSU{
    private:
    vector<int> parent_; // 用于集合关联，默认每个元素自己是一个集合。
    vector<int> rank_;   // 将孩子较少的节点合并到节点较多的节点，减少查找次数。
    public:
    DSU(int N) {
        parent_.resize(N);
        for (int i = 0; i < N; i++) // 每个元素默认是自己的集合的根
            parent_[i] = i;
        rank_.resize(N, 1);    // rank默认数为1
    }
    int find(int x) { // 每次查找，都递归进行合并，避免层数过高。
        if (parent_[x] != x)
            parent_[x] = find(parent_[x]);
        return parent_[x];
    }
    int find(int x, int &outSize) {    // 可以查找当前集合总数
        if(parent_[x] != x) parent_[x] = find(parent_[x]);
        outSize = rank_[parent_[x]];
        return parent_[x];
    }
    bool doUnion(int x, int y) {
        int xr = find(x), yr = find(y);
        if(xr == yr)
            return false;
        else if (rank_[xr] < rank_[yr]) {
            parent_[xr] = yr;
            rank_[yr] += rank_[xr];
        } else {
            parent_[yr] = xr;
            rank_[xr] += rank_[yr];
        }
        return true;
    }
};

// Go 版本
type DSU struct {
    parents []int
    ranks []int
}

// 创建DSU对象
func NewDSU(size int) (res *DSU) {
    if size <= 0 {
        return
    }

    res = &DSU{
        parents : make([]int, size),
        ranks : make([]int, size),
    }

    for i := 0; i < size; i++ {
        res.parents[i] = i
        res.ranks[i] = 1
    }
    return
}

func (p *DSU) Find(x int) (root int, err error) {
    if x < 0 || x >= len(p.parents) {
        err = errors.New("invalid index")
        return
    }

    if p.parents[x] != x {
        p.parents[x], _ = p.Find(p.parents[x])
    }
    root = p.parents[x]
    return
}

func (p *DSU) Union(x ,y int) (res bool, err error) {
    if x < 0 || x >= len(p.parents) || y < 0 || y >= len(p.parents) {
        err = errors.New("invalid index")
        return
    }

    xRoot, _ := p.Find(x)
    yRoot, _ := p.Find(y)

    if xRoot == yRoot {
        res = false
        return
    }

    if p.ranks[xRoot] >= p.ranks[yRoot] {
        p.parents[yRoot] = xRoot
        p.ranks[xRoot] += p.ranks[yRoot]
    } else {
        p.parents[xRoot] = yRoot
        p.ranks[yRoot] += p.ranks[xRoot]
    }
    res = true
    return
}

应用示例

此题目来自于 leetcode”399. Evaluate Division”，该题目有两种解法，一种是 DFS 搜索除法关系链，一种是下面这种 DSU 解法。后者在时间复杂度上有明显优势，每一次查找是 O(1)。

/*
challenge:
Equations are given in the format A / B = k, where A and B are variables represented as strings,
and k is a real number (floating point number). Given some queries, return the answers.
If the answer does not exist, return -1.0.

Example:
Given a / b = 2.0, b / c = 3.0.
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? .
return [6.0, 0.5, -1.0, 1.0, -1.0 ].

The input is: vector<pair<string, string>> equations, vector<double>& values,
vector<pair<string, string>> queries , where equations.size() == values.size(),
and the values are positive. This represents the equations. Return vector<double>.

According to the example above:

equations = [ ["a", "b"], ["b", "c"] ],
values = [2.0, 3.0],
queries = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ].


The input is always valid. You may assume that evaluating the queries will result in
no division by zero and there is no contradiction.
*/

type DSU struct {
    parent map[string]string    // node->parent of the node
    ratio map[string]float64    // node->(node value / parent value)
}

func (p *DSU) Union(divided, divisor string, value float64) {
    for _, node := range []string{divided, divisor} {
        if _, exists := p.parent[node]; !exists {
            p.parent[node] = node
            p.ratio[node] = 1.0
        }
    }
    p1, dividedRatio := p.Find(divided)
    p2, divisorRatio := p.Find(divisor)
    p.parent[p1] = p2
    p.ratio[p1] = value * divisorRatio / dividedRatio
}

func (p *DSU) Find(node string) (ancestor string, ratio float64) {
    ancestor, exists := p.parent[node]
    if !exists {
        return
    }
    if node == ancestor {
        ratio = p.ratio[node]
        return
    }

    father := p.parent[node]
    ancestor, fatherRatio := p.Find(father)
    p.parent[node] = ancestor
    p.ratio[node] = p.ratio[node] * fatherRatio
    ratio = p.ratio[node]
    return
}

func NewDSU() *DSU {
    return &DSU {
        parent : make(map[string]string),
        ratio : make(map[string]float64),
    }
}

func calcEquation(equations [][]string, values []float64, queries [][]string) []float64 {
    dsu := NewDSU()
    for i := 0; i < len(equations); i++ {
        dsu.Union(equations[i][0], equations[i][1], values[i])
    }

    res := make([]float64, 0, len(queries))
    for _, q := range queries {
        p1, r1 := dsu.Find(q[0])
        p2, r2 := dsu.Find(q[1])
        // not in dsu or not in the same set
        if p1 == "" || p2 == "" || p1 != p2 {
            res = append(res, -1.0)
        } else {
            res = append(res, r1 / r2)
        }
    }
    return res
}